Math 187 Section 3: Discrete and Foundational Mathematics I.
Instructor: Andrés Caicedo.
Contact Information: See here.
Time: MTuWF 1:40-2:30 pm.
Place: Mathematics/Geosciences building, Room 120.
Office Hours: MF 12:40-1:30 pm.
Text:
- Proof: Introduction to Higher Mathematics. By Warren W. Esty and Norah C. Esty. Fifth edition.
- The proof is in the Pudding. The Changing Nature of Mathematical Proof. By Steven G. Krantz. Springer, 2011.
Contents: From the Course Descriptions in the Department’s site:
An introduction to the language and methods of reasoning used throughout mathematics and computer science, and to selected topics in discrete mathematics. Propositional and predicate logic; elementary set theory; introduction to proof techniques including mathematical induction; functions and relations; and basic principles of elementary number theory, combinatorial enumeration, and graph theory.
There are two components to this course. First, you will learn some topics in discrete mathematics (for example, counting techniques, a bit of graph theory, and number theory). Just as important, in this course you will learn how to read (and hopefully, understand) mathematical arguments, and how to write mathematical proofs. Ideally, at the end of the course you will be able to produce a few proofs of your own.
We will cover different topics from the Proof textbook, with varying degrees of emphasis. We will cover additional topics not in the textbook, mainly on graph theory. Appropriate references will be given in that case; if needed, notes will be posted on this blog. This page will be frequently updated with detailed week-to-week descriptions, including homework assignments.
The book by Krantz discusses changes to the concept of proof through history. Many examples are presented, as well as stories about practicing mathematicians. We will cover these through the term.
Detailed week to week description:
- August 22-26. Introduction. We begin by covering material from Chapter 1, sections 1.1 and 1.2, with additional examples. Homework problems: From Section 1.1, exercises A.1-A.12, B.1-B.16, C.2.
- August 29-September 2. Sections 1.2, 4.1, 1.3. Much more on Venn Diagrams can be found on the dynamic survey by Frank Ruskey and Mark Weston at the Electronic Journal of Combinatorics site. See also the article The Search for Simple Symmetric Venn Diagrams by Frank Ruskey, Carla D. Savage, and Stan Wagon, in the Notices of the American Mathematical Society, December 2006, Volume 53, Issue 11. In reference to section 1.3, it may be useful to read section 1.4, The foundations of logic, in Krantz’s book. Quiz 1. Homework problems: Section 1.2: A.1, A.4, A.19, A.26, A.28, A.33-46; Section 4.1: Resolve the conjectures C.3-C.9. Since Monday September 5th is a holiday, the 2nd homework is due September 7th at the beginning of lecture, and we will have the 2nd quiz that day in the last 20 minutes of lecture.
- September 6-9. Sections 1.3-1.6. Please also read “Detecting cheaters” on the excellent blog by Bruce Schneier. Quiz 2. Homework problems: Section 1.4: A.1, A.8-A.11, A.18-A.20, B.5, B.7-B.9. Section 1.5: A.1-A.8. A.33-A.36, A.50, A.51, B.3, B.27.
- September 12-16. The P-vs-NP problem. Section 11.7 of Krantz’s book. Also, this handout on P, NP, and the P-vs-NP problem. Wikipedia has an excellent discussion of Boolean satisfiability, the example we are mostly focusing on. See also its page on 2-satisfiability, which is actually a problem solvable in polynomial time. Krom’s algorithm, discussed there, builds on the idea of the “resolution method”, so please read details of the method in this handout. (The handout goes into more details than we are covering now; we will revisit it later once we have talked about mathematical induction.) Quiz 3. Homework problems: Here. Due Friday September 23. (Quiz 4 will be on Tuesday as usual.)
- September 19-23. Quantifiers. Sections 2.1-2.3. Quiz 4. Homework problems: Section 2.1: A.1-A.12, B.4-B.9; Section 2.2: A.1-A.4, A.7-A.12, A.22-A.26, A.29-A.32, B.41-B.43, B.45-B.47. Recall that the first midterm is next week, on September 27.
- September 26-30. Sections 2.3, 2.5, 3.3. First midterm: Tuesday, September 27. Homework problems: Section 2.3: A.5-A.8, B.3-B.5 (note that the answer to B.5.b will be a formula in terms of both
and
), B.21, B.28, B.31, B.32, B.121; Section 2.5: B.5, B.6, B.15-B.22, B.39.
- October 3-7. Sections 3.3, 3.4, 3.5. Quiz 5. Homework problems: Section 3.4: A3, A4, A5, A7, B2, B4, B9, B17, B18, B19, C3, C5. In case you missed it, here is a link to the NOVA Profile on the brothers Chudnovsky.
- October 10-14. Sections 3.5, 6.1. Quiz 6. Homework problems: Section 3.5: A1, A4, A7, B1, B4, B5, B6, B9-B19, B24. I am not requiring that you turn in C1 or C2, but it may be a good idea to work on them. Section 6.1: A1-A7, B17-B19, B22-B24, B35, B37, B38. I have posted some extra credit problems here. Our first presentation will be this Wednesday, see here.
- October 17-21. Sections 3.5, 6.2, 6.3. Quiz 7. In case you missed it, here is a link to the TED talk by Cédric Villani. Homework problems:
- Use induction to prove that
.
- The arithmetic mean of
numbers
is their average,
. Their geometric mean is
. Show that if
and all the numbers
are positive, then
. (Actually, the result is true for all
, even if they are not powers of
, but the proof of this is more difficult.)
- The Fibonnaci numbers are given by
,
, and
. Show that
. (On the other hand, Example 4 from section 3.5 shows that
. One sometimes combines these two results, by saying that the rate of growth of the Fibonacci sequence is exponential.)
- Section 3.5: B.46, B.50.
- October 24-28. Sections 6.2, 6.3, 3.6 of the “Proof” textbook; Section 11.10 of Krantz’s book. Quiz 8. Homework problems: Section 6.2: A.9-A.16, B.8, B.9. Solve two of B.22-B.27. B-30. Section 3.6: A.3, B.6, B.7, B.10. B.26, B.29, B.31, B.32, B.41. Our second presentation will be this Wednesday, see here. Here is a link to the official page of the Alan Turing Year. Recall that the second midterm is next week, on November 2.
- October 31-November 4. The second midterm is Wednesday, November 2; please do not forget to bring a blue book. There will be a review on Nov. 1. On Friday, Nov.4, we will start Section 6.3, on prime numbers. There is no homework due next week. Here are our grader’s solutions for last week’s homework.
- November 7-11. Sections 6.3, 6.4. Quiz 9. Homework problems: Section 6.3: A.1-A.6, B.24, B.28-B.31, B.40, B.44, B.52, B.55. Section 6.4: A.2-A.6, A.9, B.1, B.8, B.20, B.21, C.1.
- November 14-18. Basic combinatorics (counting). We will be following the book Counting and configurations, by J. Herman, R. Kucera, and J. Simsa; Springer, Canadian Mathematical Society (2003). I will distribute a handout, on their sections 1.1, 1.2, 1.5(1-5). Quiz 10. Homework problems: From the handout: 1.3.1, 1.6.1, 1.6.2, 2.3.1, 2.3.3, 2.3.5, 2.6.2, 2.9.1, 2.9.5, 2.12.1, 2.12.4, 2.12.7, 2.19.1-6, 5.5.1.
- November 21-25. Thanksgiving break. Happy thanksgiving!
- November 28-December 2. The binomial theorem. Basic theory of functions. For the binomial theorem, we will follow Section 1.7 of the book Combinatorics by R. Merris; John Wiley & Sons, Inc. (2003). For functions, see Sections 5.1 and 5.2 of the Proof book. Quiz 11. Homework problems: From the handout: 1(b),(e),(i), 2(a),(d),(f),(i), 4, 6, 7, 11 (Hint for 11(b): You may argue by induction, and in the inductive step use the binomial theorem and 11(a). [There are other arguments that do not require induction.]) From the Proof book: 5.1.A1, A4, A7, A14, A17, A18, B1, B39.
- December 5-9. Dead week. We will cover Section 5.2 and, depending on time, the basic theory of relations, including equivalence relations (I will distribute a handout with these topics). We will have a review at the end. (Optional) Quiz 12. Optional homework: 5.2.A1, A6, A8, A12, B22, B23, B24. Remember the final exam is Wednesday, December 14, 1-3 pm. This exam is cumulative; please bring a blue book.
- December 14. Final exam. It was a pleasure having you in my class!
Presentations: Here is the list of all presentations we had, including links to some of them.
Prerequisites: Math 143, Math 147, or satisfactory placement score.
Quizzes: There will be weekly quizzes, on the last 20 minutes of Tuesday’s lecture (not on August 24). Each quiz will evaluate, roughly, the material covered the previous week. You are not allowed to only show up about 20 minutes before the end of the lecture in order to take the quiz; if you show up only for the quiz, your score is 0. If you fail to take a quiz, it will be scored as 0. The lowest score will be dropped.
For each quiz, I will provide you with a page with the question(s) printed. You may use this page to solve the questions. You need to bring any additional pieces of paper you may require. If a quiz will require more than 20 minutes, I will inform in advance, both in lecture and in this page.
Notes from class, textbooks, and calculators, are allowed during exams and quizzes. Bring your own pen, pencil, eraser, etc.
Homework: There is weekly homework, due Tuesdays at the beginning of lecture; you are welcome to turn in your homework early, but I will not accept homework past Tuesdays at 1:40 pm. The homework covers the material from the previous week, and it is a good idea to work daily on the homework problems corresponding to the material covered that day. During office hours, you are welcome to ask about problems from the assigned sets (or any other problems you find interesting). Frequently, some (but not necessarily all) of the problems from the quizzes will be fairly close, if not outright identical, to homework problems.
Following Otis Kenny‘s suggestion, your homework must follow the format developed by the mathematics department at Harvey Mudd College; it does not need to be typeset. You will find that format at this link. If you do not use this style, your homework will be graded as 0.
Your grader is Joanna Thompson, her email address is joannathompson@u.boisestate.edu. Feel free to contact her if you have questions about grading decisions; however, you should talk to me instead if you feel something was graded incorrectly/too harshly/unfairly/etc.
Extra credit: I may assign a few challenging problems through the term. Additionally, you may volunteer to present in class one of the stories covered in Krantz’s book, or a similar story. Let me know, and we will schedule a 10-15 minute presentation.
Exams: There will be 2 in-class exams and a comprehensive final exam.
- Exam 1: Tuesday, September 27.
- Exam 2: Wednesday, November 2.
- Final exam: Wednesday, December 14. 1-3 pm. This exam is cumulative.
Dates and times are non-negotiable. Failure to take a exam will be graded as a score of 0. There will be no make up for the final exam. For the in-class exams, a make up can be arranged if I am notified prior to the exam date and a valid reason is presented; keep in mind that make up exams will be more difficult than regular in-class exams.
You need to bring blue books to the exams.
Grading:
- Quizzes: 20%. (Each quiz weighs the same towards the final grade.)
- Homework: 20%. (Each homework set weighs the same towards the final grade.)
- Exam 1: 20%.
- Exam 2: 20%.
- Final exam: 20%.
Your grade is then determined by a linear scale:
- If your final score is 90 or higher, you receive an A.
- If it is 80 or higher, you receive at least a B.
- If it is 70 or higher, you receive at least a C.
- If it is 60 or higher, you receive a D.
- There will be a curve at the end (which may increase your grade, never decrease it), and plus and minus grades might be used for grades near the top or bottom of a grade range.
Attendance: Not required, but encouraged. Any material covered in lecture, or assigned as homework, may be used in quizzes and exams, even if it is not discussed in the textbooks. I will use this website to post any additional information, and encourage you to use the comments feature, but (in general) I will not post here standard content covered in the textbooks and in class. If you leave a comment, please use your full name, which will simplify my life filtering spam out.
Hello Dr. Caicedo, I had a couple questions. First, is there anywhere I can find some of the answers to the textbook questions? Or someway I can verify if I’m doing these right? Also, would you prefer questions concerning homework problems posted here or somewhere else?
Hi Kevin.
I don’t think the answers are available, sorry. One way to verify if what you are doing is right is to check during office hours. You may also want to check with other students, usually many doubts can be solved quickly that way.
Questions about homework problems are fine here, but if the question is about verifying that your approach works, or whether your answer is right, it is better if you ask me directly or by email.
Hello Dr. Caicedo,
I am having trouble getting started on Section 3.4 problems B4, B9, C3, and C5. Would you offer some hints on how to approach these? Are there prior results that must be considered? Are there multiple cases that need to be considered? Any help on getting started on these problems would be much appreciated. Thanks.
Hi David,
Here is a hint for B4: You want to argue by contradiction, assuming that there are integers and
and  that satisfy the given equation. Now, divide the argument into two cases: Can
that satisfy the given equation. Now, divide the argument into two cases: Can  be even? Can it be odd?
be even? Can it be odd?
For B9, the hint is to try to argue following closely the proof we gave for the irrationality of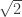 , so you need to examine that proof, and see whether you can “adapt it” to prove the irrationality of
, so you need to examine that proof, and see whether you can “adapt it” to prove the irrationality of 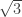 . The key point in that proof was when we arrived at an equation of the form
. The key point in that proof was when we arrived at an equation of the form 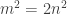 and we used it to conclude, first that
and we used it to conclude, first that  was even and, then, that
was even and, then, that  was also even. If you follow the same idea in this case, you will now arrive instead at an equation of the form
was also even. If you follow the same idea in this case, you will now arrive instead at an equation of the form 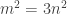 . Now, rather than deducing that
. Now, rather than deducing that  is even, try to deduce from this that
is even, try to deduce from this that  must be a multiple of 3.
must be a multiple of 3.
How? Well, try a proof by contradiction! If is not a multiple of 3, then when you divide it by 3, it leaves a remainder, which will be 1 or 2, right, so
is not a multiple of 3, then when you divide it by 3, it leaves a remainder, which will be 1 or 2, right, so  has the form
has the form 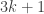 or
or  . Show that in either case,
. Show that in either case,  is *not* a multiple of 3.
is *not* a multiple of 3.
For C3, you argue by contradiction, assuming that the equation has a rational root. Following the hint the book gives, we may assume the root is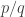 where
where  and
and  have no common factors. Multiply the equation by
have no common factors. Multiply the equation by 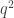 , you should arrive at something like
, you should arrive at something like  .
.
Now, the argument requires 3 steps: 1. Show that must be odd. To show this, suppose instead that
must be odd. To show this, suppose instead that  is even, and derive a contradiction. Here you will need to use the assumption that
is even, and derive a contradiction. Here you will need to use the assumption that 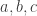 are odd integers.
are odd integers.
2. Show that must be odd. To do this, the argument should be very similar to what you did in the previous step.
must be odd. To do this, the argument should be very similar to what you did in the previous step.
3. Now that you know that and
and  are odd, and that
are odd, and that 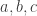 are also odd, explain why it is not possible for
are also odd, explain why it is not possible for  to be 0.
to be 0.
Once you finish the third step, you have reached a contradiction: You have that , and you also have that it is *not* equal to 0.
, and you also have that it is *not* equal to 0.
For C5, it may be useful to introduce some notation, because you want to examine what a sum of three consecutive positive integers looks like. Say, the first one is . What are the other two? What is their sum? Now that you have a formula for the sum, can this be a prime number? Be careful with this last step, you may have to consider a couple of cases.
. What are the other two? What is their sum? Now that you have a formula for the sum, can this be a prime number? Be careful with this last step, you may have to consider a couple of cases.
Hope this helps.
Hello Dr. Caicedo,
I’m not certain that I’m doing these problems correctly, but if I am, I have a question. For example, with problem 1e, “What is the coeficient of x^5 in the binamial expansion of (1+2x)^7”. Is the desired coeficient just the result of (7¦5), i.e. 21? Or after factoring out the 4 from 4x^2, so 84?
(1+2x)^7:
∑_(k=0 -> 7)〖(7¦5) (1^5) (2x)^2 〗
= [7!/((5!)(2!))] * (4x^2 )
= 21(4x^2 )
= 84x^2
Thanks,
Dave
Hi Dave, it is not just , but it is not 84 either (you want the coefficient of
, but it is not 84 either (you want the coefficient of  , not of
, not of 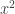 ), it should be
), it should be  or something like this.
or something like this.