We showed that every well-ordered set is isomorphic to a unique ordinal. The proof uses replacement in an essential way.
Example. 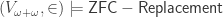 and in this model there are well-ordered sets not isomorphic to any ordinal. We will return to this example in the future.
and in this model there are well-ordered sets not isomorphic to any ordinal. We will return to this example in the future.
We defined natural numbers in the context of set theory and showed that  , the first limit ordinal, is the set of natural numbers.
, the first limit ordinal, is the set of natural numbers.
We explained how we understand (proper) classes within  . Other formalizations of set theory allow one to handle classes as actual objects, for example Gödel-Bernays-von Neumann set theory,
. Other formalizations of set theory allow one to handle classes as actual objects, for example Gödel-Bernays-von Neumann set theory,  , the system in which Gödel originally presented his proof of the consistency of the axiom of choice and the generalized continuum hypothesis. See here for a brief description of
, the system in which Gödel originally presented his proof of the consistency of the axiom of choice and the generalized continuum hypothesis. See here for a brief description of  . One can show that
. One can show that 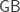 is conservative over
is conservative over  .
.
Finally, we stated versions of the theorem of transfinite induction and proved a version of the theorem of transfinite recursion: Given any  there is a unique
there is a unique  such that for all ordinals
such that for all ordinals  ,
, 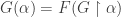 .
.
This result is very useful. It allows us, for example, to define operations on the ordinals by recursion. The easiest example is perhaps the definition of addition of ordinals: Let 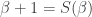 be the successor of
be the successor of  .
.
To see that there is a unique function satisfying these conditions, one can show that this is a particular case of the theorem. For this, define  as follows:
as follows:  unless
unless  is a sequence. If
is a sequence. If  , let
, let  . If
. If  for some
for some  , let
, let  . If
. If 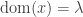 is a limit ordinal, let
is a limit ordinal, let 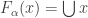 . The function
. The function 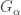 whose existence is granted by the theorem is precisely
whose existence is granted by the theorem is precisely  .
.
We also stated (without proof) Hartog’s theorem. The following definition will be useful.
Definition. A set  is finite iff there is a natural number
is finite iff there is a natural number  such that
such that  . Otherwise, it is infinite.
. Otherwise, it is infinite.
(This is our official defintion. There are several possible ways of defining infinite sets, and they are not necessarily equivalent without choice. One such alternative, Dedekind infinite, is presented in Exercise 2 of the Homework.)
For completeness, I include a proof of Hartog’s theorem. Recall:
Theorem (Hartog). ( ) For any set
) For any set  , let
, let  there is an injection of
there is an injection of  into
into 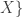 . Then
. Then  is an ordinal.
is an ordinal.
Proof. Clearly the class  is transitive (which for ordinals simply means, closed under initial segments). So it suffices to see that it is a set. This uses replacement.
is transitive (which for ordinals simply means, closed under initial segments). So it suffices to see that it is a set. This uses replacement.
Notice that if  is a bijection, then there is a well-ordering of
is a bijection, then there is a well-ordering of  in order type
in order type  : Simply set
: Simply set 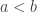 in
in  iff there are
iff there are 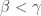 in
in  such that
such that  and
and  .
.
By von Neumann’s theorem, conversely, if 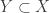 and
and  is well-ordered, then there is an ordinal
is well-ordered, then there is an ordinal  such that
such that 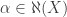 as witnessed by the unique order isomorphism
as witnessed by the unique order isomorphism  . Hence,
. Hence,  coincides with the class of ordinals
coincides with the class of ordinals  such that there is a subset
such that there is a subset  of
of  and a well-ordering of
and a well-ordering of  isomorphic to
isomorphic to  .
.
Since a well-ordering of  is just a subset of
is just a subset of  , it follows that
, it follows that  is a set, by replacement.
is a set, by replacement. 
The following (important) observation is needed in the homework, I will return to it in Tuesday’s lecture: Suppose now that  itself is well-orderable. Then
itself is well-orderable. Then  . Because since
. Because since  is well-orderable, there is an ordinal
is well-orderable, there is an ordinal 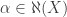 (thus,
(thus,  ) and a bijection
) and a bijection  . Hence,
. Hence,  . However, if
. However, if  is a bijection, we can well-order
is a bijection, we can well-order  isomorphically to
isomorphically to  by setting
by setting 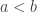 in
in  iff
iff  as ordinals. But this would imply that
as ordinals. But this would imply that  , a contradiction.
, a contradiction.
Remark. In the statement of Exercise 1 in the Homework,  is defined as the union of the set we are calling
is defined as the union of the set we are calling  here. This makes no difference whenever
here. This makes no difference whenever  is infinite (as one can easily check), so feel free to use either version, we will discuss this issue in lecture.
is infinite (as one can easily check), so feel free to use either version, we will discuss this issue in lecture.
), and showed how to compute under
the function
.
nothing can be said about the exponential function
beyond monotonicity and König’s theorem.
is strong limit, then
is regular and smaller than
.
is not the first counterexample to
.



 Posted by andrescaicedo
Posted by andrescaicedo