305 -6. Rings, ideals, homomorphisms

March 13, 2009

It will be important to understand the subfields of a given field; this is a key step in figuring out whether a field {{\mathbb Q}^{p(x)}} is an extension by radicals or not. We need some “machinery” before we can develop this understanding.

Recall:

Definition 1 A ring is a set {R} together with two binary operations {+,\times} on {R} such that:

  1. {+} is commutative.
  2. There is an additive identity {0.}
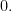
  3. Any {a} has an additive inverse {-a.}
  4. {+} is associative.
  5. {\times} is associative.
  6. {\times} distributes over {+,} both on the right and on the left.

Read the rest of this entry »

Leave a Comment » | 305: Abstract Algebra I | Tagged: , , , | Permalink
Posted by andrescaicedo

305 -Extensions by radicals (2)

March 5, 2009

2. Extensions by radicals

 

Last lecture we defined {{\mathbb F}^{p(x)}} where {{\mathbb F}} is a subfield of a field {{\mathbb K},} all the roots of the polynomial {p(x)} are in {{\mathbb K},} and all the coefficients of {p(x)} are in {{\mathbb F}.} Namely, if {r_1,\dots,r_n} are the roots of {p,} then {{\mathbb F}^{p(x)}={\mathbb F}(r_1,\dots,r_n),} the field generated by {r_1,\dots,r_n} over {{\mathbb F}.}

The typical examples we will consider are those where {{\mathbb F}={\mathbb Q},} {{\mathbb K}={\mathbb C},} and the coefficients of {p(x)} are rational or in fact, integers.

Read the rest of this entry »

2 Comments | 305: Abstract Algebra I | Tagged: , , | Permalink
Posted by andrescaicedo