305 -Fields (5)

February 27, 2009

At the end of last lecture we stated a theorem giving an easy characterization of subfields of a given field {\mathbb F}. We begin by proving this result.

Theorem 18. Suppose {\mathbb F} is a field and S\subseteq{\mathbb F}. If S satisfies the following 5 conditions, then S s a subfield of {\mathbb F}:

  1. S is closed under addition.
  2. S is closed under multiplication.
  3. -a\in S whenever a\in S.
  4. a^{-1}\in S whenever a\in S and a\ne0.
  5. S has at least two elements.

Read the rest of this entry »

2 Comments | 305: Abstract Algebra I | Tagged: , , , , | Permalink
Posted by andrescaicedo

305 -Homework set 4

February 22, 2009

I am not happy with the solutions I received for problems 4 and 5 of Homework set 2 so, for this new set, due March 2 at the beginning of lecture, you must redo these two problems correctly. As usual, the homework policy is detailed in the syllabus. However, there are a few points I want to emphasize:

  • Although I have so far allowed collaboration, each student should write their own solutions. If a group of students collaborate in a problem, they should indicate so at the beginning of their solutions. 

Let me explain this a bit. I do not simply mean that each of you has to write or type your own set of solutions. Of course I expect that, but I expect more than that. When you write your solutions, you should do this on your own. I do not want to see exactly the same mistakes in different people, exactly the same notation, exactly the same equations. If I see it ever again, even if it is not intentional, I will not allow collaboration any longer. Collaboration means that you work together and help one another and give suggestions to one another. Once you have come up with a solution, then collaboration stops and you should write your own version of what was found. 

  • Also, if references are consulted, they should be listed. This means you should mention the books you look at that gave you ideas. This means you should give the name of the book, the author, the edition, the theorem you are using or quoting or being inspired by. Similarly, if you find ideas online, mention the webpage where you found them. 

Now, and this is very important: Your solutions are your own. It may be that by accident in some book you run into the solution of a problem I assigned. This is fine, as long as it is not done intentionally, and I trust your honesty in this regard. Remember that you are bound by an honor code. It is not acceptable to copy the solution the book gives, not even if you give a complete reference that makes it clear that the solution is not your own. If you find a useful idea in a book, make sure you understand it before you use it. Just copying it down will not be acceptable, even if you change notation or the order in which the idea is presented. If you find a solution in a book, and you do not understand it, you will be better off not attempting to use it.  

If I see that the two points above (or any of the details of the homework policy) are not followed, I may change the grading policy and increase the number of quizzes we will have and the percentage they contribute to your total grade. 

Please make sure your solutions are reasonably self contained. If you use a result we have not shown in class you need to provide a proof. Please make sure you turn in your homework on time. This means at the beginning of lecture, not at the end of lecture or in the middle of lecture.

6 Comments | 305: Abstract Algebra I | Tagged: | Permalink
Posted by andrescaicedo

305 -Fields (4)

February 20, 2009

Suppose that {\mathbb F} is a field and that S\subset{\mathbb F}. It may be that S is also a field, using the same operations of {\mathbb F}. For example, if {\mathbb F}={\mathbb R}, then we could have S={\mathbb Q}.

Definition 15. If {\mathbb F} is a field and S\subset{\mathbb F}, we say that S is a subfield of {\mathbb F} if S is a field with the operations of {\mathbb F}.

Read the rest of this entry »

1 Comment | 305: Abstract Algebra I | Tagged: | Permalink
Posted by andrescaicedo

305 -Homework set 3

February 18, 2009

This set is due February 25 at the beginning of lecture. Consult the syllabus for details on the homework policy.

1. Show directly that there is no field of 6 elements. (“Directly” means, among other things, that you cannot use the facts mentioned without proof at the end of lecture 4.3.)

2. Construct a field of size 8. Once you are done, verify that all its elements satisfy the equation x^8-x=0.

3. Solve exercises 36–38 from Chapter 4 of the book.

4. Is the set \{a+b\root 4\of 2 : a,b\in{\mathbb Q}\} a field with the usual +,\times,0,1?

1 Comment | 305: Abstract Algebra I | Tagged: | Permalink
Posted by andrescaicedo

305 -Fields (3)

February 18, 2009

At the end of last lecture we arrived at the question of whether every finite field is a {\mathbb Z}_p for some prime p.

In this lecture we show that this is not the case, by exhibiting a field of 4 elements. We also find some general properties of finite fields. Finite fields have many interesting applications (in cryptography, for example), but we will not deal much with them as our focus through the course is on number fields, that we will begin discussing next lecture.

We begin by proving the following result:

Lemma 13. Suppose that {\mathbb F} is a finite field. Then there is some natural number n>0 such that the sum of n ones vanishes, 1+\dots+1=0. The least such n is a prime that divides the size of the field. 

Read the rest of this entry »

2 Comments | 305: Abstract Algebra I | Tagged: , | Permalink
Posted by andrescaicedo

580 -Cardinal arithmetic (6)

February 17, 2009

3. The Galvin-Hajnal theorems.

In this section I want to present two theorems of Galvin and Hajnal that greatly generalize Silver’s theorem. I focus on a “pointwise” (or everywhere) result, that gives us information beyond the pointwise theorems from last lecture, like Corollary 23. Then I state a result where the hypotheses, as in Silver’s theorem, are required to hold stationarily rather than everywhere. From this result, the full version of Silver’s result can be recovered.

Both results appear in the paper Fred Galvin, András Hajnal, Inequalities for Cardinal Powers, The Annals of Mathematics, Second Series, 101 (3), (May, 1975), 491–498, available from JSTOR, that I will follow closely. For the notion of \kappa-inaccessibility, see Definition II.2.20 from last lecture.  

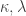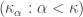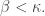Theorem 1. Let \kappa,\lambda be uncountable regular cardinals, and suppose that \lambda is \kappa-inaccessible. Let (\kappa_\alpha:\alpha<\kappa) be a sequence of cardinals such that \prod_{\alpha<\beta}\kappa_\alpha<\aleph_\lambda for all \beta<\kappa. Then also \prod_{\alpha<\kappa}\kappa_\alpha<\aleph_\lambda.

The second theorem will be stated next lecture. Theorem 1 is a rather general result; here are some corollaries that illustrate its reach:  

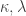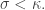Corollary 2. Suppose that \kappa,\lambda are uncountable regular cardinals, and that \lambda is \kappa-inaccessible. Let \tau be a cardinal, and suppose that \tau^\sigma<\aleph_\lambda for all cardinals \sigma<\kappa. Then also \tau^\kappa<\aleph_\lambda.

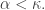
Proof. Apply Theorem 1 with \kappa_\alpha=\tau for all \alpha<\kappa. {\sf QED}

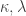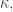Corollary 3. Suppose that \kappa,\lambda are uncountable regular cardinals, and that \lambda is \kappa-inaccessible. Let \tau be a cardinal of cofinality \kappa, and suppose that 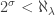2^\sigma<\aleph_\lambda for all cardinals \sigma<\tau. Then also 2^\tau<\aleph_\lambda.

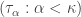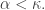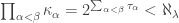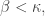Proof. Let (\tau_\alpha:\alpha<\kappa) be a sequence of cardinals smaller than \tau such that \tau=\sum_\alpha\tau_\alpha, and set \kappa_\alpha=2^{\tau_\alpha} for all \alpha<\kappa. Then \prod_{\alpha<\beta}\kappa_\alpha=2^{\sum_{\alpha<\beta}\tau_\alpha}<\aleph_\lambda for all \beta<\kappa, by assumption. By Theorem 1, \prod_{\alpha<\kappa}\kappa_\alpha=2^{\sum_\alpha\tau_\alpha}=2^\tau<\aleph_\lambda as well. {\sf QED}    

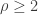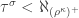Corollary 4. Let \kappa,\rho,\tau be cardinals, with \rho\ge2 and \kappa regular and uncountable. Suppose that \tau^\sigma<\aleph_{(\rho^\kappa)^+} for all cardinals 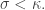\sigma<\kappa. Then also \tau^\kappa<\aleph_{(\rho^\kappa)^+}.

Proof. This follows directly from Corollary 2, since \lambda=(\rho^\kappa)^+ is regular and \kappa-inaccessible. {\sf QED}

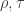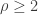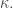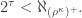
Corollary 5. Let \rho,\tau be cardinals, with \rho\ge2 and \tau of uncountable cofinality \kappa. Suppose that 2^\sigma<\aleph_{(\rho^\kappa)^+} for all cardinals \sigma<\tau. Then also 2^\tau<\aleph_{(\rho^\kappa)^+}.

Proof. This follows directly from Corollary 3 with 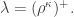\lambda=(\rho^\kappa)^+. {\sf QED}

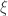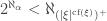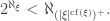
Corollary 6. Let \xi be an ordinal of uncountable cofinality, and suppose that 2^{\aleph_\alpha}<\aleph_{(|\xi|^{{\rm cf}(\xi)})^+} for all \alpha<\xi. Then also 2^{\aleph_\xi}<\aleph_{(|\xi|^{{\rm cf}(\xi)})^+}.

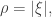
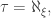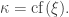
Proof. This follows from Corollary 5 with \rho=|\xi|, \tau=\aleph_\xi, and \kappa={\rm cf}(\xi). {\sf QED}

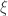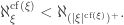
Corollary 7. Let \xi be an ordinal of uncountable cofinality, and suppose that \aleph_\alpha^\sigma<\aleph_{(|\xi|^{{\rm cf}(\xi)})^+} for all cardinals \sigma<{\rm cf}(\xi) and all \alpha<\xi. Then also \aleph_\xi^{{\rm cf}(\xi)}<\aleph_{(|\xi|^{{\rm cf}(\xi)})^+}.

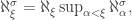Proof. This follows from Corollary 4: If \sigma<{\rm cf}(\xi), then \aleph_\xi^\sigma=\aleph_\xi\sup_{\alpha<\xi}\aleph_\alpha^\sigma, by Theorem II.1.10 from lecture II.2. But 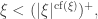\xi<(|\xi|^{{\rm cf}(\xi)})^+, so both 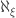\aleph_\xi and \sup_{\alpha<\xi}\aleph_\alpha^\sigma are strictly smaller than \aleph_{(|\xi|^{{\rm cf}(\xi)})^+}. {\sf QED} 

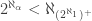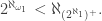
Corollary 8. If 2^{\aleph_\alpha}<\aleph_{(2^{\aleph_1})^+} for all \alpha<\omega_1, then also  2^{\aleph_{\omega_1}}<\aleph_{(2^{\aleph_1})^+}.

Proof. By Corollary 5. {\sf QED}

Corollary 9.  If \aleph_\alpha^{\aleph_0}<\aleph_{(2^{\aleph_1})^+} for all \alpha<\omega_1, then also  \aleph_{\omega_1}^{\aleph_1}<\aleph_{(2^{\aleph_1})^+}.

Proof. By Corollary 7. {\sf QED}

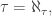Notice that, as general as these results are, they do not provide us with a bound for the size of 2^\tau for \tau the first cardinal of uncountable cofinality that is a fixed point of the aleph sequence, \tau=\aleph_\tau, not even under the assumption that \tau is a strong limit cardinal. 

Read the rest of this entry »

10 Comments | 580: Topics in set theory | Tagged: | Permalink
Posted by andrescaicedo

580 -Cardinal arithmetic (5)

February 13, 2009

At the end of last lecture we defined club sets and showed that the diagonal intersection of club subsets of a regular cardinal is club.

Definition 10. Let \alpha be a limit ordinal of uncountable cofinality. The set S\subseteq\alpha is stationary in \alpha iff S\cap C\ne\emptyset for all club sets C\subseteq\alpha. 

For example, let \lambda be a regular cardinal strictly smaller than {\rm cf}(\alpha). Then S^\alpha_\lambda:=\{\beta<\alpha : {\rm cf}(\beta)=\lambda\} is a stationary set, since it contains the \lambda-th member of the increasing enumeration of any club in \alpha. This shows that whenever {\rm cf}(\alpha)>\omega_1, there are disjoint stationary subsets of \alpha. Below, we show a stronger result. The notion of stationarity is central to most of set theoretic combinatorics. 

Fact 11. Let S be stationary in \alpha.

  1. S is unbounded in \alpha.
  2. Let C be club in \alpha. Then S\cap C is stationary. 

Proof. 1. S must meet \kappa\setminus\alpha for all \alpha and is therefore unbounded.

2. Given any club sets C and D, (S\cap C)\cap D=S\cap(C\cap D)\ne\emptyset, and it follows that S\cap C is stationary. {\sf QED}

Read the rest of this entry »

6 Comments | 580: Topics in set theory | Tagged: , , , , , , | Permalink
Posted by andrescaicedo

305 -Fields (2)

February 13, 2009

We continue from last lecture. Examination of a few particular cases finally allows us to complete Example 6. The answer to whether {\mathbb Z}_n (with the operations and constants defined last time) is a field splits into three parts. The first is straightforward.

Lemma 10. For all positive integers n>1, {\mathbb Z}_n satisfies all the properties of fields except possible the existence of multiplicative inverses. \Box.

This reduces the question of whether {\mathbb Z}_n is a field to the problem of finding multiplicative inverses, which turns out to be related to properties of n.
Read the rest of this entry »

1 Comment | 305: Abstract Algebra I | Tagged: , | Permalink
Posted by andrescaicedo

580 -Cardinal arithmetic (4)

February 11, 2009

2. Silver’s theorem.

From the results of the previous lectures, we know that any power \kappa^\lambda can be computed from the cofinality and gimel functions (see the Remark at the end of lecture II.2). What we can say about the numbers \gimel(\lambda) varies greatly depending on whether \lambda is regular or not. If \lambda is regular, then \gimel(\lambda)=2^\lambda. As mentioned on lecture II.2, forcing provides us with a great deal of freedom to manipulate the exponential function \kappa\mapsto 2^\kappa, at  least for \kappa regular. In fact, the following holds:

Theorem 1. (Easton). If {\sf GCH} holds, then for any definable function F from the class of infinite cardinals to itself such that:

  1. F(\kappa)\le F(\lambda) whenever \kappa\le\lambda, and
  2. \kappa<{\rm cf}(F(\kappa)) for all \kappa,

there is a class forcing {\mathbb P} that preserves cofinalities and such that in the extension by {\mathbb P} it holds that 2^\kappa=F^V(\kappa) for all regular cardinals \kappa; here, F^V is the function F as computed prior to the forcing extension. \Box

For example, it is consistent that 2^\kappa=\kappa^{++} for all regular cardinals \kappa (as mentioned last lecture, the same result is consistent for all cardinals, as shown by Foreman and Woodin, although their argument is significantly more elaborate that Easton’s). There is almost no limit to the combinations that the theorem allows: We could have 2^\kappa=\kappa^{+16} whenever \kappa=\aleph_\tau is regular and \tau is an even ordinal, and 2^\kappa=\kappa^{+17} whenever \kappa=\aleph_\tau for some odd ordinal \tau. Or, if there is a proper class of weakly inaccessible cardinals (regular cardinals \kappa such that \kappa=\aleph_\kappa) then we could have 2^\kappa= the third weakly inaccessible strictly larger than \kappa, for all regular cardinals \kappa, etc.

Morally, Easton’s theorem says that there is nothing else to say about the gimel function on regular cardinals, and all that is left to be explored is the behavior of \gimel(\lambda) for singular \lambda. In this section we begin this exploration. However, it is perhaps sobering to point out that there are several weaknesses in Easton’s result.

Read the rest of this entry »

2 Comments | 580: Topics in set theory | Tagged: , , , , , , , | Permalink
Posted by andrescaicedo

305 -4. Fields.

February 11, 2009

Definition 1. Let {\mathbb F} be a set. We say that the quintuple ({\mathbb F},+,\times,0,1) is a field iff the following conditions hold:

  1. +:{\mathbb F}\times {\mathbb F}\to {\mathbb F}.
  2. \times:{\mathbb F}\times {\mathbb F}\to {\mathbb F.} (We say that {\mathbb F} is closed under addition and multiplication.)
  3. 0,1\in{\mathbb F}.
  4. 0\ne1.
  5. Properties 1–9 of the Theorem from last lecture hold with elements of {\mathbb F} in the place of complex numbers, {}0 in the place of \hat0, and {}1 in the place of \hat1.

Read the rest of this entry »

4 Comments | 305: Abstract Algebra I | Tagged: , | Permalink
Posted by andrescaicedo

« Previous Entries