Here is the midterm.
1. Hooke’s law says that the force required to stretch a spring a distance of  units from its natural length is given by
units from its natural length is given by  where
where  is a constant that only depends on the spring.
is a constant that only depends on the spring.
We are told that for the spring of problem 1 we have  where units of distance are measured in meters, and forces in Newtons. This means that
where units of distance are measured in meters, and forces in Newtons. This means that  or
or 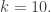 The work required to stretch the spring 10 m beyond its natural length is then
The work required to stretch the spring 10 m beyond its natural length is then 
2. We are given a curve with equation  and asked to rotate about the
and asked to rotate about the  -axis the segment where
-axis the segment where  To find the area of the resulting surface, we can consider splitting the surface into little shells. A typical `thin’ shell, at height
To find the area of the resulting surface, we can consider splitting the surface into little shells. A typical `thin’ shell, at height  has surface area
has surface area  where
where  is the radius of the shell, in this case just the value of
is the radius of the shell, in this case just the value of  corresponding to
corresponding to 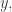 i.e.,
i.e.,  Also,
Also, 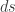 is here the arc length element, given by
is here the arc length element, given by 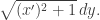
We have:  so
so 
Hence the requested area is given by 
This expression reduces to 
3. We are given the region bounded by the curve  and the lines
and the lines  and
and  We rotate it about the
We rotate it about the  -axis, and are asked to find the volume of the resulting solid. A first attempt is to use the washer method. A typical thin washer consists of a slice of the solid for a fixed value of
-axis, and are asked to find the volume of the resulting solid. A first attempt is to use the washer method. A typical thin washer consists of a slice of the solid for a fixed value of  and with thickness
and with thickness  Its volume is
Its volume is  Here,
Here, 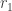 is the exterior radius, which in this case is always 2, and
is the exterior radius, which in this case is always 2, and  is the interior radius, given by
is the interior radius, given by  This means the washer contributes
This means the washer contributes  of the full volume, and adding all of them together we obtain
of the full volume, and adding all of them together we obtain  The upper limit of 4 comes from observing that the curves
The upper limit of 4 comes from observing that the curves  and
and  cross precisely at the point
cross precisely at the point 
Unfortunately, this integral is not one of the given expressions.
So we attempt a different approach, using now the shell method. Now a typical thin shell is obtained by fixing a height  and rotating about the
and rotating about the  -axis the slice of the figure of thickness
-axis the slice of the figure of thickness 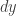 and height
and height  Its volume is
Its volume is  where
where  is the radius of the shell, in this case
is the radius of the shell, in this case  and
and  is the length of the shell, in this case
is the length of the shell, in this case  We thus proceed to express
We thus proceed to express  in terms of
in terms of  Since
Since 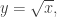 then
then  Hence the thin shell contributes
Hence the thin shell contributes  of the full volume, and the volume is obtained by adding all these contributions, obtaining
of the full volume, and the volume is obtained by adding all these contributions, obtaining  This is expression (c).
This is expression (c).
4. The length of the curve  for
for 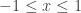 is given by the integral
is given by the integral  In this case,
In this case,  so
so 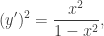 and
and 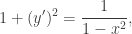 so the integral reduces to
so the integral reduces to  which is expression (b).
which is expression (b).
[There is a small problem with this integral, though, because the denominator vanishes at both endpoints. Later, in Chapter 7, we will learn how to handle integrals of this kind. Note that if the question had been to actually find the length, there is an easier method: The curve is half a circumference of radius 1, so the length is  ]
]
5. (a) The differential equation 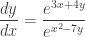 can be rewritten as
can be rewritten as  which is clearly separable. (T)
which is clearly separable. (T)
(b) The area swept by 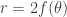 for
for  is four times the area swept by
is four times the area swept by  Intuitively, we are making lengths twice as long, and areas carry two dimensions of length. Think of the area of a square of side 2, for example. Formally, we can check that this is the case: The area swept by the first curve is given by
Intuitively, we are making lengths twice as long, and areas carry two dimensions of length. Think of the area of a square of side 2, for example. Formally, we can check that this is the case: The area swept by the first curve is given by 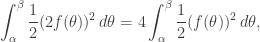 while the area swept by the second curve is given by
while the area swept by the second curve is given by  (T)
(T)
(c) The half life of a given element is 3 days. This means that 50% of the given amount of the element has decayed after 3 days. After 3 more days, another 25% would have decayed. After 3 more days, another 12.5%. After 3 more days, another 6.25%. Since  the given statement is clearly true.
the given statement is clearly true.
A longer way of checking the same is by recalling that the total amount of the element that remains after time  if originally the amount is
if originally the amount is  is given by
is given by  where
where  is a given constant. Measure
is a given constant. Measure  in days. We are told that
in days. We are told that  so
so 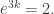 Then
Then  and
and  (T)
(T)



 Posted by andrescaicedo
Posted by andrescaicedo