2. The ultrapower construction
The study of ultrapowers originates in model theory, although it has found applications both in algebra and in analysis. However, it is accurate to say that it is mainly exploited in set theory. Here I present the basic idea, showing its close connection to the study of measurable cardinals, defined last lecture.
Suppose first that 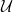 is an ultrafilter over a set
is an ultrafilter over a set  We want to define the ultrapower of the universe
We want to define the ultrapower of the universe 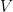 of sets by
of sets by 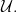 The basic idea is to consider the product of
The basic idea is to consider the product of  many copies of the structure
many copies of the structure 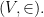 We want to “amalgamate” them somehow into a new structure
We want to “amalgamate” them somehow into a new structure 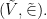 For this, we look for the “typical” properties of the elements
For this, we look for the “typical” properties of the elements 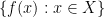 of each “thread”
of each “thread” 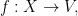 and add an element
and add an element 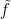 to
to  whose properties in
whose properties in  are precisely these typical properties. We use
are precisely these typical properties. We use 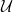 to make this precise, by saying that a property
to make this precise, by saying that a property 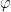 is typical of the range of
is typical of the range of  iff
iff  This leads us to the following definition, due to Dana Scott, that adapts the ultrapower construction to the context of proper classes:
This leads us to the following definition, due to Dana Scott, that adapts the ultrapower construction to the context of proper classes:
Definition 1 Let 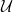 be an ultrafilter over a nonempty set
be an ultrafilter over a nonempty set  We define the ultrapower
We define the ultrapower 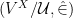 of
of 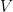 by
by 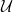 as follows:
as follows:
For  say that
say that

This is easily seen to be an equivalence relation. We would like to make the elements of 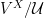 to be the equivalence classes of this relation. Unfortunately, these are all proper classes except for the trivial case when
to be the equivalence classes of this relation. Unfortunately, these are all proper classes except for the trivial case when  is a singleton, so we cannot within the context of our formal theory form the collection of all equivalence classes.
is a singleton, so we cannot within the context of our formal theory form the collection of all equivalence classes.
Scott’s trick solves this problem by replacing the class of  with
with
![\displaystyle [f]:=\{g:X\rightarrow V: g=_{\mathcal U}f\mbox{ and }{\rm rk}(g)\mbox{ is least possible}\}.](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Bf%5D%3A%3D%5C%7Bg%3AX%5Crightarrow+V%3A+g%3D_%7B%5Cmathcal+U%7Df%5Cmbox%7B+and+%7D%7B%5Crm+rk%7D%28g%29%5Cmbox%7B+is+least+possible%7D%5C%7D.+&bg=ffffff&fg=000000&s=0&c=20201002)
Here, as usual, 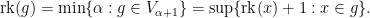 All the “classes”
All the “classes” ![{[f]}](https://s0.wp.com/latex.php?latex=%7B%5Bf%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) are now sets, and we set
are now sets, and we set ![{V^X/{\mathcal U}=\{[f]: f:X\rightarrow V\}.}](https://s0.wp.com/latex.php?latex=%7BV%5EX%2F%7B%5Cmathcal+U%7D%3D%5C%7B%5Bf%5D%3A+f%3AX%5Crightarrow+V%5C%7D.%7D&bg=ffffff&fg=000000&s=0&c=20201002)
We define 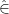 by saying that for
by saying that for 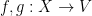 we have
we have
![\displaystyle [f]\hat\in[g]\mbox{ iff }\{x\in X:f(x)\in g(x)\}\in{\mathcal U}.](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Bf%5D%5Chat%5Cin%5Bg%5D%5Cmbox%7B+iff+%7D%5C%7Bx%5Cin+X%3Af%28x%29%5Cin+g%28x%29%5C%7D%5Cin%7B%5Cmathcal+U%7D.+&bg=ffffff&fg=000000&s=0&c=20201002)
(It is easy to see that 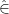 is indeed well defined, i.e., if
is indeed well defined, i.e., if  and
and 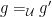 then
then  iff
iff 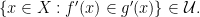 )
)
(The ultrapower construction is more general than as just defined; what I have presented is the particular case of interest to us.) The remarkable observation, due to  is that this definition indeed captures the typical properties of each thread in the sense described above:
is that this definition indeed captures the typical properties of each thread in the sense described above:
Read the rest of this entry »
is a sequence of finite nonempty sets, and
then
has size
for any nonprincipal ultrafilter
on
then
His argument is a very nice application of non-standard analysis. The case that interests us is easier.



 Posted by andrescaicedo
Posted by andrescaicedo