116c- Lecture 18

May 30, 2008

We briefly discussed relative constructibility and compared the models L[x] where x is exclusively treated as a predicate with the models L(x) where x is an element. In particular, L[x] is a model of choice but L(x) may fail to be.

An amusing application of the fact that L[x]\models{\sf AC} is that the result of Exercise 3 from Homework 7 holds in {\sf ZF}, although the proof I wrote there uses choice. Namely, work in {\sf ZF} and consider two well-orderings of a set X. We can assume that X is an ordinal \alpha and the first well-ordering is \in. Let \prec be the second well-ordering. Then \prec\in L[\prec] (since \prec is a set of ordered pairs of ordinals). In L[\prec], where choice holds, (and therefore also in V) there is a subset of \alpha of the same size as \alpha and where \prec coincides with \in.

Question. Find a `choice-free’ argument for Exercise 3. 

The main example we will consider of a model of the form L(x) is L({\mathbb R}), due to its connection with determinacy.

We introduced the setting to discuss determinacy, namely infinite 2-person games with perfect information. We proved the Gale-Stewart theorem that open games are determined and discussed Martin’s extension to Borel games. A nice reference for the proof of Martin’s result (using the idea of `unraveling‘, which reduces any Borel game to an open game in a different space) is Kechris’s book on descriptive set theory.

2 Comments | 116c: Set theory | Permalink
Posted by andrescaicedo

116c- Homework 8

May 29, 2008

Homework 8

Due Thursday, June 5 at 2:30 pm. 

Leave a Comment » | 116c: Set theory | Tagged: | Permalink
Posted by andrescaicedo

116c- Lecture 17

May 29, 2008

We verified that the sets L_\alpha form a continuous increasing sequence and are transitive. It follows that the reflection theorem holds for the L_\alpha and L. Arguing in {\sf ZF}, we proved that L is a model of {\sf ZF}, and the reflection theorem allowed us to simplify the proof in a few points.

We then proceeded to argue that L is also a model of choice. In fact, there is a globally definable well-ordering of L. It is worth emphasizing that the well-ordering is a very natural one, as we simply proceed to enumerate the sets in L in the order in which their membership is verified. The definitions of the sequence of sets L_\alpha and of this well-ordering are absolute, and we used this to prove that L is a model of the statement “V=L,” and so is any L_\alpha, for \alpha limit. Moreover, the well-ordering of L, when restricted to L_\alpha, coincides with its interpretation inside L_\alpha.

An easy induction shows that for \alpha infinite, |L_\alpha|=|\alpha|. An argument using the Mostowski collapsing theorem allowed us to prove Gödel’s condensation lemma: If X\prec L_\alpha for \alpha a limit ordinal, then X is isomorphic to some L_\beta. These two facts combine to provide a proof that {\sf GCH} holds in L.

Remark. These arguments prove that {\rm Con}({\sf ZF}) implies {\rm Con}({\sf ZFC}), but they also indicate that showing that {\rm Con}({\sf ZF}) implies {\rm Con}({\sf ZF}+\lnot{\sf AC}) ought to be more complicated. The reason is that the absoluteness of the construction of L implies that if M is a transitive proper class model of {\sf ZF}, then L\subseteq M and in fact L^M=L, i.e., the result of running the construction of L from the point of view of M is L itself. But, since V=L holds in L, we cannot prove in {\sf ZF} that there is a non-constructible set. If we tried to establish the consistency of {\sf ZF} with the negation of choice by a similar method, namely, the construction of a transitive class model M of {\sf ZF}+\lnot{\sf AC}, then running the construction inside L would give us that L=L^{M^L}\subseteq M^L\subseteq L, so M^L=L, which would be a contradiction, since we are assuming that (provably in {\sf ZF}) M is a model of \lnot{\sf AC} but L is a model of choice.

This also suggests that in order to show that {\sf AC} is independent of {\sf ZF}, one should try first to show that V\ne L is consistent with {\sf ZF}. The remarkable solution found by Paul Cohen in 1963, the method of forcing, allows us to prove the consistency of both statements, and also to do this while working with transitive models. The method of forcing is beyond the scope of this course, but good explanations can be found in a few places, there is for example a book by Cohen himself, or look at Kunen’s book mentioned at the beginning of the course. Richard Zach has compiled in his blog a list of papers providing an introduction to the method (search for `forcing’).

Leave a Comment » | 116c: Set theory | Permalink
Posted by andrescaicedo

116c- Lecture 16

May 24, 2008

We showed that \Delta_1 formulas are absolute among transitive models of (enough) set theory, and used this to prove that satisfiability for transitive sets is absolute. More precisely, let {\rm Sat}(a,b,c) mean that a is a transitive set M, b codes a formula \varphi(\vec x), c is a tuple \vec X of elements of M, and M\models\varphi(\vec X). Then {\rm Sat}(a,b,c) is \Delta_1. Using this and the reflection theorem we can conclude that \Delta_1 is actually the extent of absoluteness in set theory, meaning that whenever there is a finite S such that \phi is absolute for transitive models of S, then \phi is \Delta_1.

We exhibited a few formulas that are not absolute. For example, “x is a cardinal” and “x=V_\alpha,” although both are \Pi_1 and therefore relativize downwards.

The main application of the absoluteness of satisfiability is that it allows us to define the constructible hierarchy and Gödel’s constructible universe L.

Remark. On the other hand, we cannot define in general satisfiability for transitive classes, by Tarski’s undefinability of truth theorem. The difference with the case of sets is that with sets the recursive definition of M\models involves several bounded quantifiers, ranging over finite powers of M. With general proper classes M, these quantifiers would be unbounded. An easy inductive argument shows that we can define partial satisfiability predicates (and therefore partial truth predicates), meaning that for each natural number n and each class M we can find a \Sigma_n formula that defines satisfiability for \Sigma_n formulas with respect to M; although we cannot in general find a uniform definition that works simultaneously for all n.  

Leave a Comment » | 116c: Set theory | Permalink
Posted by andrescaicedo

116c- Lecture 15

May 21, 2008

We presented a list of statements, definable relations, functions, and constants, that are absolute for transitive models of enough set theory. We showed that absolute functions are closed under composition, although \Delta_0 functions are not. We also verified that being a well-ordering is absolute. The same argument actually shows:

Theorem. The statement “R is a well-founded relation on A” is absolute for transitive models of {\sf ZF}-{\sf Powerset}.

This is a key result very useful in a variety of situations. Notice that we are not claiming that being well-orderable is absolute; in fact, it is not. The difference is that in the first case we are given a witness to the well-orderability, and claim that no matter in which transitive model the witness is observed, in all of them it has the property of being a well-ordering. The second case only states that there is a witness, and a given model may very well fail to produce such a witness unless it is a model of the axiom of choice.

Leave a Comment » | 116c: Set theory | Permalink
Posted by andrescaicedo

116c- Homework 7

May 20, 2008

Homework 7

Due Wednesday, May 28 at 2:30 pm.

Update. I present here a quick sketch of the solution of Exercise 3.(b). See Lecture 18, where it is shown that the result actually holds in {\sf ZF}, although the proof uses choice.

 Let < and \prec be two well-orderings of a set X. We want to find a subset of X of the same size as X where the two well-orderings coincide. Let \kappa=|X|. By combining with an isomorphism between (X,<) and its order type, we may assume that X is an ordinal and <=\in. By restricting attention to the subset \kappa of X, we may assume \prec is a well-ordering of \kappa. By further restricting to the subset of \kappa of order type \kappa under \prec, we may assume that {\rm ot}(\kappa,\prec)=\kappa as well. 

Assume first that \kappa is regular. The result follows easily. The desired set Y can be built by a straightforward recursion: Given \beta<\kappa and (\gamma_\alpha:\alpha<\beta) a sequence of elements of \kappa increasing under both well-orderings, regularity ensures that the sequence is bounded under both well-orderings, and we can find \gamma_\beta which is larger than all the previous \gamma_\alpha under both orderings.

The argument for \kappa singular is slightly more delicate. Namely, we may not be able to carry out the construction above since the sequence could be unbounded in one of the orderings when {\rm cf}(\beta)={\rm cf}(\kappa). We circunvent the problem by only considering ordinals \beta whose cofinality is larger than the cofinality of \kappa. Notice that if an increasing sequence of order type \beta  is unbounded in an ordinal of cofinality \gamma, then {\rm cf}(\beta)={\rm cf}(\gamma).

To implement this idea, let (\kappa_i:i<{\rm cf}(\kappa)) be an increasing sequence of regular cardinals cofinal in \kappa, with {\rm cf}(\kappa)<\kappa_0. Consider the subset \kappa_0. It must contain a subset of size \kappa_0 where \prec coincides with \in. By the remark above, this subset B is bounded in (\kappa,\prec). Let A denote the shortest initial segment of (\kappa,\prec) containing B. By removing from \kappa the set \kappa_0\cup A, we are left with a set of size \kappa, and any ordinal there is larger than the elements of B under both orderings. The induction continues this way, by considering at stage i a set of size \kappa_i.

Leave a Comment » | 116c: Set theory | Tagged: | Permalink
Posted by andrescaicedo

116c- Lecture 14

May 16, 2008

We defined absoluteness of formulas with respect to two classes M\subset N; for example, every \Delta_0 formula is absolute with respect to M and V, if M is transitive. Once we establish a sufficiently long list of properties that are absolute with respect to a transitive model of (enough of) {\sf ZFC} and V, we will be able to prove a few relative consistency results. The main application will be in the proof that Gödel’s constructible universe L is a model of {\sf ZF} (and of choice and {\sf GCH}), but a few other examples will be presented as well.

We proved the reflection theorem and some of its consequences, in particular, that no consistent extension of {\sf ZF} is finitely axiomatizable.

An important application of these techniques is the use of basic model theoretic tools to establish combinatorial facts. Some examples will be explored in the next homework set.

Leave a Comment » | 116c: Set theory | Permalink
Posted by andrescaicedo

116c- Homework 6

May 14, 2008

Homework 6

Due Wednesday, May 21 at 2:30 pm.

Update. Since Wednesday, May 21 is ditch day, the homework is now due Thursday, May 22 at 2:30 pm. 

Update. Here is a quick sketch of the solution of exercise 3:

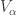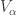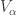Assume in {\sf ZF} that the power set of any ordinal is well-orderable. We want to conclude that choice holds, i.e., that every set is well-orderable. A natural strategy is to proceed inductively, showing that each V_\alpha is well-orderable: Clearly, if the result is true, each V_\alpha would be well-orderable. 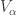But also, given any set x, it belongs to some V_\alpha and, since the latter is transitive, in fact x\subseteq V_\alpha and therefore x is well-orderable as well. The strategy is suggested by the fact that for all \alpha, V_{\alpha+1}={\mathcal P}(V_\alpha), so a well-ordering of V_\alpha gives us a well-ordering of 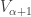V_{\alpha+1} thanks to our initial assumption.

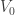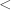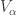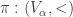
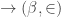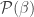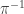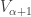We argue by induction: Clearly V_0 is well-ordered by the well-ordering <_0=\emptyset. Given a well-ordering < of V_\alpha, there is a unique ordinal \beta and a unique order isomorphism \pi : (V_\alpha , <) \to (\beta, \in). By assumption, {\mathcal P}(\beta) is well-orderable, and any well-ordering of it induces (via \pi^{-1}) a well-ordering of V_{\alpha+1}.

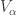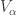We are left with the task of showing that V_\alpha is well-orderable for \alpha limit. The natural approach is to patch together the well-orderings of the previous V_\beta into a well-ordering of V_\alpha. This approach meets two obstacles.

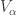The first, and not too serious, one, is that the well-orderings of different V_\beta are not necessarily compatible, so we need to be careful on how we “patch them together. ” The natural solution to this obstacle is to simply order the sets as they appear inside V_\alpha. More precisely, define 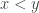x<y for x,y\in V_\alpha, iff

  • Either {\rm rk}(x)<{\rm rk}(y), or else
  • {\rm rk}(x)={\rm rk}(y)=\beta, say, and if <_{\beta+1} is the well-ordering of V_{\beta+1}, then x<_{\beta+1}y.

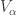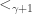It is easy to see that this is indeed a well-ordering of V_\alpha: Given a non-empty A\subseteq V_\alpha,  let \gamma be least so that A has an element of rank \gamma. Then the <_{\gamma+1}-first among these elements would be the 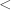<-least element of A. 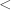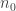Or we could argue that there are no infinite <-descending chains: If (x_n:n<\omega) is such a chain then, since ({\rm rk}(x_n):n<\omega) is a non-increasing sequence of ordinals, there must be n_0 such that all 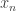x_n with n\ge n_0 have the same rank \beta. 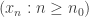But then (x_n:n\ge n_0) would be an infinite <_{\beta+1}-descending sequence, contradicting that <_{\beta+1} is a well-ordering.

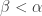The second obstacle is more serious. Namely, the assumption is simply that there is a well-ordering of each {\mathcal P}(\delta), not that there is any canonical way of choosing one. 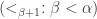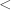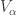In order for the argument above to work, we need not just that each V_\beta for \beta<\alpha is well-orderable, but in fact we need to have selected a sequence (<_{\beta+1}:\beta<\alpha) of well-orderings of the V_{\beta+1}, with respect to which we proceeded to define the well-ordering < of V_\alpha.

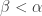The way we began the proof suggests a solution: When we argued that it suffices to well-order each V_\gamma, we considered an arbitrary set x and noticed that if x\subseteq V_\beta, then a well-ordering of V_\beta gives us a well-ordering of x. Similarly, given \alpha limit, if we can find \delta large enough so each |V_\beta| for \beta<\alpha is below \delta, then we can use a well-ordering of {\mathcal P}(\delta) to induce the required well-ordering <_\beta.  

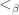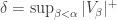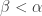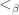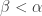We now proceed to implement this idea: Let \delta=\sup_{\beta<\alpha}|V_\beta|^+. (Notice that this makes sense since, inductively, each V_\beta with \beta<\alpha is well-orderable and therefore isomorphic to a unique cardinal.) Let <^* be a well-ordering of {\mathcal P}(\delta). We use <^* to define a sequence (<_\beta:\beta<\alpha) so that <_\beta well-orders V_\beta for all \beta<\alpha. We use recursion on 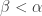\beta<\alpha to define this sequence. Again, <_0=\emptyset. 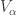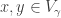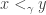At limit stages \gamma<\alpha we copy the strategy with which we tried to well-order V_\alpha to define <_\gamma: For x,y\in V_\gamma, set x<_\gamma y iff

  • Either {\rm rk}(x)<{\rm rk}(y), or else
  • {\rm rk}(x)={\rm rk}(y)=\beta, say, and x<_{\beta+1}y.

Finally, given 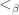<_\beta, we describe how to define <_{\beta+1}: Let \xi=\xi_\beta be the unique ordinal such that there is an order isomorphism

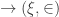\pi : (V_\beta,<_\beta) \to (\xi,\in).

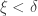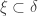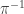Since |\xi|=|V_\beta|, then \xi<\delta, so \xi\subset\delta and the well-ordering <^* of {\mathcal P}(\delta) also well-orders {\mathcal P}(\xi). Via \pi^{-1}, this induces the well-ordering <_{\beta+1} of V_{\beta+1} we were looking for.

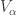Equipped with the sequence (<_\beta:\beta<\alpha) we can now proceed to well-order V_\alpha as explained above. This completes the proof. {\sf QED}

3 Comments | 116c: Set theory | Tagged: | Permalink
Posted by andrescaicedo

116c- Lecture 13

May 13, 2008

We explored well-founded relations and proved a generalization of the recursion theorem to well-founded, set like relations. The main application of this result is the Mostowski collapsing theorem.

Finally, we defined relativizations and explained how they are useful to establish relative consistency results; absolute consistency results being precluded by Gödel’s second incompleteness theorem.

1 Comment | 116c: Set theory | Permalink
Posted by andrescaicedo

116c- Lecture 12

May 8, 2008

We completed the proof of Silver’s theorem. Silver’s argument, as understood by Baumgartner and Prikry, started a whole new series of results that culminated in Shelah’s celebrated pcf theory. See

T. Jech, Singular cardinals and the pcf theory, The Bulletin of Symbolic Logic 1(4) (1995), 408-424

for an introduction (without proofs) and historical remarks, or

M. Burke, M. Magidor, Shelah’s pcf theory and its applications, Ann. Pure Appl. Logic 50 (3) (1990), 207-254

for a more technical introduction , including proofs. Jech’s paper is available through JSTOR.

We defined the cumulative hierarchy {\sf WF}=\bigcup_{\alpha\in{\sf ORD}}V_\alpha, proved its basic properties and showed that V={\sf WF}.

Leave a Comment » | 116c: Set theory | Permalink
Posted by andrescaicedo

« Previous Entries