580 -Cardinal arithmetic (5)

February 13, 2009

At the end of last lecture we defined club sets and showed that the diagonal intersection of club subsets of a regular cardinal is club.

Definition 10. Let \alpha be a limit ordinal of uncountable cofinality. The set S\subseteq\alpha is stationary in \alpha iff S\cap C\ne\emptyset for all club sets C\subseteq\alpha. 

For example, let \lambda be a regular cardinal strictly smaller than {\rm cf}(\alpha). Then S^\alpha_\lambda:=\{\beta<\alpha : {\rm cf}(\beta)=\lambda\} is a stationary set, since it contains the \lambda-th member of the increasing enumeration of any club in \alpha. This shows that whenever {\rm cf}(\alpha)>\omega_1, there are disjoint stationary subsets of \alpha. Below, we show a stronger result. The notion of stationarity is central to most of set theoretic combinatorics. 

Fact 11. Let S be stationary in \alpha.

  1. S is unbounded in \alpha.
  2. Let C be club in \alpha. Then S\cap C is stationary. 

Proof. 1. S must meet \kappa\setminus\alpha for all \alpha and is therefore unbounded.

2. Given any club sets C and D, (S\cap C)\cap D=S\cap(C\cap D)\ne\emptyset, and it follows that S\cap C is stationary. {\sf QED}

Read the rest of this entry »

6 Comments | 580: Topics in set theory | Tagged: , , , , , , | Permalink
Posted by andrescaicedo

580 -Cardinal arithmetic (4)

February 11, 2009

2. Silver’s theorem.

From the results of the previous lectures, we know that any power 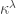\kappa^\lambda can be computed from the cofinality and gimel functions (see the Remark at the end of lecture II.2). What we can say about the numbers \gimel(\lambda) varies greatly depending on whether \lambda is regular or not. If \lambda is regular, then \gimel(\lambda)=2^\lambda. As mentioned on lecture II.2, forcing provides us with a great deal of freedom to manipulate the exponential function \kappa\mapsto 2^\kappa, at  least for \kappa regular. In fact, the following holds:

Theorem 1. (Easton). If 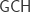{\sf GCH} holds, then for any definable function F from the class of infinite cardinals to itself such that:

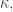
  1. F(\kappa)\le F(\lambda) whenever \kappa\le\lambda, and
  2. \kappa<{\rm cf}(F(\kappa)) for all \kappa,

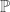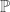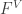there is a class forcing {\mathbb P} that preserves cofinalities and such that in the extension by {\mathbb P} it holds that 2^\kappa=F^V(\kappa) for all regular cardinals \kappa; here, F^V is the function F as computed prior to the forcing extension. \Box

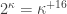For example, it is consistent that 2^\kappa=\kappa^{++} for all regular cardinals \kappa (as mentioned last lecture, the same result is consistent for all cardinals, as shown by Foreman and Woodin, although their argument is significantly more elaborate that Easton’s). There is almost no limit to the combinations that the theorem allows: We could have 2^\kappa=\kappa^{+16} whenever \kappa=\aleph_\tau is regular and \tau is an even ordinal, and 2^\kappa=\kappa^{+17} whenever \kappa=\aleph_\tau for some odd ordinal \tau. 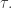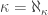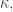Or, if there is a proper class of weakly inaccessible cardinals (regular cardinals \kappa such that \kappa=\aleph_\kappa) then we could have 2^\kappa= the third weakly inaccessible strictly larger than \kappa, for all regular cardinals 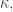\kappa, etc.

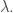Morally, Easton’s theorem says that there is nothing else to say about the gimel function on regular cardinals, and all that is left to be explored is the behavior of \gimel(\lambda) for singular \lambda. In this section we begin this exploration. However, it is perhaps sobering to point out that there are several weaknesses in Easton’s result.

Read the rest of this entry »

2 Comments | 580: Topics in set theory | Tagged: , , , , , , , | Permalink
Posted by andrescaicedo

580 -Cardinal arithmetic (3)

February 9, 2009

It is easy to solve negatively the question immediately following Homework problem 5 on lecture II.1. I asked whether if X is Dedekind-finite but {\mathcal P}(X) is Dedekind-infinite, then it followed that there is an infinite Dedekind-finite set Y such that {\mathcal P}(Y)\preceq X.

To exhibit a counterexample, it is enough to know that it is consistent to have an infinite Dedekind finite set X that is the countable union of finite sets (in fact, sets of size 2). Notice that \omega is a surjective image of X, so {\mathcal P}(X) is Dedekind-infinite. Suppose that {\mathcal P}(Y)\preceq X. Then certainly Y\preceq X, so Y is a countable union of finite sets Y_n. If Y is infinite then Y_n\ne\emptyset for infinitely many values of n. But then \omega is also a surjective image of Y, so \omega (and in fact P(\omega)) injects into {\mathcal P}(Y) and therefore into X, contradiction.

At the end of last lecture we showed Theorem 10, a general result that allows us to compute products \kappa^\lambda for infinite cardinals \kappa,\lambda, namely:

Let \kappa and \lambda be infinite cardinals. Let \tau=\sup_{\rho<\kappa}|\rho|^\lambda. Then 

\displaystyle \kappa^\lambda=\left\{\begin{array}{cl} 2^\lambda & \mbox{if }\kappa\le 2^\lambda,\\ \kappa\cdot\tau & \mbox{if }\lambda<{\rm cf}(\kappa),\\ \tau & \begin{array}{l}\mbox{if }{\rm cf}(\kappa)\le\lambda,2^\lambda<\kappa,\mbox{ and }\\ \rho\mapsto|\rho|^\lambda\mbox{ is eventually constant below }\kappa,\end{array}\\ \kappa^{{\rm cf}(\kappa)} & \mbox{otherwise.}\end{array}\right.

Read the rest of this entry »

5 Comments | 580: Topics in set theory | Tagged: , , , | Permalink
Posted by andrescaicedo