When studying local extreme points of functions of several (real) variables, the textbook asks in one of the exercises to consider the polynomial
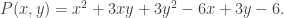
Here we have  and
and  , so the only critical point of
, so the only critical point of  is
is 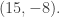 Since
Since  and the Hessian of
and the Hessian of  is
is 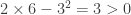 , it follows that
, it follows that  is a local minimum of
is a local minimum of  and, since it is the only critical point, it is in fact an absolute minimum with
and, since it is the only critical point, it is in fact an absolute minimum with 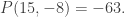
 being a polynomial, it is reasonable to expect that there is an algebraic explanation as for why
being a polynomial, it is reasonable to expect that there is an algebraic explanation as for why  is its minimum, and why it lies at
is its minimum, and why it lies at  . After all, this is what happens in one variable: If
. After all, this is what happens in one variable: If  and
and 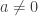 , then
, then

and obviously  has a minimum at
has a minimum at  , and this minimum is
, and this minimum is 
The polynomial  of the example above can be analyzed this way as well. A bit of algebra shows that we can write
of the example above can be analyzed this way as well. A bit of algebra shows that we can write
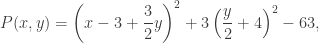
and it follows immediately that  has a minimum value of
has a minimum value of  , achieved precisely when both
, achieved precisely when both  and
and  , i.e, at
, i.e, at 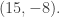
(One can go further, and explain how to go in a systematic way about the `bit of algebra’ that led to the representation of  as above, but I will leave that for a future occasion.)
as above, but I will leave that for a future occasion.)
What we did with  is not a mere coincidence. Hilbert’s 17th of the 23 problems of his famous address to the Second International Congress of Mathematicians in Paris, 1900, asks whether every polynomial
is not a mere coincidence. Hilbert’s 17th of the 23 problems of his famous address to the Second International Congress of Mathematicians in Paris, 1900, asks whether every polynomial  with real coefficients which is non-negative for all (real) choices of
with real coefficients which is non-negative for all (real) choices of 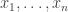 is actually a sum of squares of rational functions. (A rational function is a quotient of polynomials.) A nonnegative polynomial is usually called positive definite, but I won’t use this notation here.
is actually a sum of squares of rational functions. (A rational function is a quotient of polynomials.) A nonnegative polynomial is usually called positive definite, but I won’t use this notation here.
If Hilbert’s problem had an affirmative solution, this would provide a clear explanation as for why  is non-negative.
is non-negative.
Read the rest of this entry »
We begin by proving this result.
is a field and
If
satisfies the following 5 conditions, then
s a subfield of
is closed under addition.
is closed under multiplication.
whenever
whenever
and
has at least two elements.



 Posted by andrescaicedo
Posted by andrescaicedo