116c- Lecture 20

We showed that implies a weak version of choice, , namely, every countable family of non-empty sets of reals admits a choice function. This implies that is regular and suffices to develop classical analysis in a straightforward fashion (in particular, to construct Lebesgue measure and to prove its basic properties).

Coupled with the fact that all sets of reals have the perfect set property, this implies that for any real and therefore is strongly inaccessible in for any real . 

We closed the course by showing that, in fact, is a measurable cardinal. We proved this result of Solovay by showing Martin’s result that the “cone measure” is indeed a non-atomic measure on the structure of the Turing degrees and then “pulling back” this measure to .

Finally, given any measurable cardinal , let be a (-complete, non-principal) measure on . Then is a model of choice in which is measurable. In particular,  

Since, under choice, any measurable cardinal is strongly inaccessible and the limit of strongly inaccessible cardinals, this shows that has significant consistency strength.

116c- Lecture 19

As discussed during Lecture 13, for the theories one encounters when studying set theory, no absolute consistency results are possible, and we rather look for relative consistency statements.  For example, the theories “There is a weakly inaccessible cardinal” and “There is a strongly inaccessible cardinal” are equiconsistent. This means that a weak theory (much less than suffices) can prove . Namely: is a subtheory of , so its inconsistency implies the inconsistency of . Assume is inconsistent and fix a proof of an inconsistency from . Then a proof of an inconsistency from  can be found by showing that each is a theorem of , and this argument can be carried out in a theory (such as ) where the syntactic manipulations of formulas that this involves are possible.

It is a remarkable empirical fact that the combinatorial statements studied by set theorists can be measured against a linear scale of consistency, calibrated by the so called large cardinal axioms, of which strongly inaccessible cardinals are perhaps the first natural example. Hypotheses as unrelated as the saturation of the nonstationary ideal or determinacy have been shown equiconsistent with extensions of by large cardinals. One direction (that models with large cardinals generate models of the hypothesis under study) typically involves the method of forcing and won’t be discussed further here. The other direction, just as in the very simple example of weak vs strong inaccessibility, typically requires showing that certain transitive classes (like ) must have large cardinals of the desired sort. We will illustrate these ideas by obtaining large cardinals from determinacy in the last lecture of the course. 

We defined the axiom of determinacy . It contradicts choice but it relativizes to the model . This is actually the natural model to study and, in fact, from large cardinals one can prove that .

We illustrated basic consequences of for the theory of the reals by showing that it implies that every set of reals has the perfect set property (and therefore a version of is true under ). Similar arguments give that implies that all sets of reals have the Baire property and are Lebesgue measurable. In the last lecture of the course we will use the perfect set property of sets of reals to show that the consistency of implies the consistency of strongly inaccessible cardinals.        

Relativizations of P vs NP

In Relativizations of the 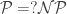question by Theodore Baker, John Gill and Robert Solovay, SIAM J. Comput. 4 (1975), no. 4, 431-442 (available through JSTOR) it is shown that the question of whether P equals NP cannot be solved with the kind of arguments typical in computability theory, since these arguments relativize to Turing machines with oracles. Among the results shown there, two oracles and are found such that and . I discussed these results during 117c, the course on decidability in computability theory.

There has been some recent attempts (not very successful, and not too serious in my opinion) to show that the P vs NP question is independent of or even stronger systems. Apparently, part of the motivation for trying to show independence comes from the results in the Baker-Gill-Solovay paper.

I reproduce below a posting by Timothy Chow to the Foundations of Mathematics list where this motivation is shown lacking.

[FOM] Amusing observation about independence of complexity results
Thursday, May 22, 2008 8:33 PM
From: Timothy Y. Chow

Here is an amusing observation regarding the idea that the existence of contradictory relativizations of assertions such as 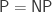is evidence that said assertions are independent of some strong theory.  I doubt this observation is new, but I haven’t seen it explicitly before.

We can write down (thanks to Levin, I think) an explicit machine with the property that, if 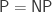, then solves in polynomial time. (Essentially multitasks over all polytime algorithms until it jackpots.)

Suppose now that a statement such as

“ correctly solves in at most steps on length- inputs”

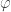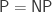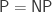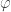is independent of (for example).  The statement is stronger than the statement that , but we might imagine that if is independent of then something like will also be independent of .

Now 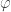is , so if it is independent of then it is true, and therefore 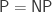.  It follows that , by the time hierarchy theorem for example.

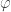This line of reasoning can itself be formalized, and this shows that in some system call it that is slightly stronger than , we can prove “if is independent of , then .” This in turn means that if we can prove “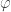 is independent of ” in , then we certainly can’t prove “ is independent of .”

Informally speaking, the upshot is that since we know that , it is probably too much to expect that both “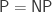” and “” are provably independent of strong systems.  On the other hand, both “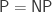” and “” admit contradictory relativizations.  So it seems we should should be wary of drawing too tight a connection between contradictory relativizations and logical independence.

Tim