1. Colorings of pairs. I
There are several possible ways in which one can try to generalize Ramsey’s theorem to larger cardinalities. We will discuss some of these generalizations in upcoming lectures. For now, let’s highlight some obstacles.
Theorem 1 ( -Kakutani)
-Kakutani)  In fact,
In fact, 
Proof: Let 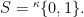 Let
Let ![{F:[S]^2\rightarrow\kappa}](https://s0.wp.com/latex.php?latex=%7BF%3A%5BS%5D%5E2%5Crightarrow%5Ckappa%7D&bg=ffffff&fg=000000&s=0&c=20201002) be given by
be given by

Then, if 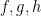 are distinct, it is impossible that
are distinct, it is impossible that 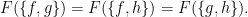

Theorem 2 (Sierpi\’nski)  In fact,
In fact, 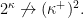
Proof: With 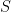 as above, let
as above, let ![{F:[S]^2\rightarrow2}](https://s0.wp.com/latex.php?latex=%7BF%3A%5BS%5D%5E2%5Crightarrow2%7D&bg=ffffff&fg=000000&s=0&c=20201002) be given as follows: Let
be given as follows: Let 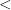 be a well-order of
be a well-order of 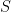 in order type
in order type 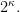 Let
Let  be the lexicographic ordering on
be the lexicographic ordering on 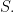 Set
Set

Lemma 3 There is no  -increasing or decreasing
-increasing or decreasing 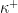 -sequence of elements of
-sequence of elements of 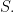
Proof: Let 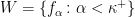 be a counterexample. Let
be a counterexample. Let  be least such that
be least such that  has size
has size  and let
and let ![{Z\in[W]^{\kappa^+}}](https://s0.wp.com/latex.php?latex=%7BZ%5Cin%5BW%5D%5E%7B%5Ckappa%5E%2B%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) be such that if
be such that if  then
then 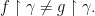 To simplify notation, we will identify
To simplify notation, we will identify 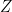 and
and  For
For 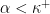 let
let  be such that
be such that  but
but  By regularity of
By regularity of  there is
there is 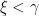 such that
such that  for
for 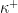 many
many 
But if  and
and 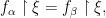 then
then 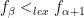 iff
iff  so
so  It follows that
It follows that  has size
has size  contradicting the minimality of
contradicting the minimality of 

The lemma implies the result: If  has size
has size 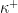 and is
and is  -homogeneous, then
-homogeneous, then 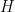 contradicts Lemma 3.
contradicts Lemma 3. 
Now I want to present some significant strengthenings of the results above. The results from last lecture exploit the fact that a great deal of coding can be carried out with infinitely many coordinates. Perhaps surprisingly, strong anti-Ramsey results are possible, even if we restrict ourselves to colorings of pairs.
Read the rest of this entry »
-Rado theorem
or larger) can be ensured, at the cost of starting with a larger domain. The following famous result was originally shown by
and Rado using tree arguments (with
lowered to
in the conclusion). We give instead an elementary substructures argument due to Baumgartner, Hajnal and
which proves the stronger version. For
a cardinal let
-Rado) Let
be a regular cardinal and let
Then
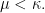



 Posted by andrescaicedo
Posted by andrescaicedo