At the end of last lecture, we showed Theorem 7, König’s lemma, stating that if for all
then
We begin by looking at some corollaries:
Corollary 8.
- If
is a limit ordinal and
is a strictly increasing sequence of nonzero cardinals, then
- If
is an
-indexed sequence of nonzero cardinals and
for all
then
- (Cantor)
- For any infinite
, one has
Proof. 1. Notice that for all
, so
by König’s lemma. But, by an obvious injection,
2. Let If
for all
then König’s lemma gives us that
3. Use König’s lemma with ,
and
for all
Then
4. Let be a cofinal function. Let
and
for all
Note that
and
5. but, by 4.,
Note that once one decodes the argument, the proof of Cantor’s theorem above is exactly the same as the usual proof. On the other hand, Corollary 8.5 gives us more information and begins to show that the notion of cofinality is quite relevant in the study of cardinal arithmetic; much more dramatic illustrations of this claim are shown below. König’s lemma is the first genuinely new result in cardinal arithmetic (with choice) past Cantor’s theorem. For example, Specker’s result in Section I.5 and the Halbeisen-Shelah theorem in Section I.6 are both trivial once is assumed.
Some of the results that follow are available elsewhere in this blog, but I include them here to make these notes reasonably self-contained.
Definition. A cardinal is strong limit iff
for all cardinals
Notice that the name is justified, since any strong limit is in particular ( or) a limit cardinal, i.e., an
with
a limit ordinal.
Of course, is a strong limit cardinal and, if
holds below
then
is also strong limit. Without this assumption, examples of strong limit cardinals can be found by iterating the power set operation. More precisely, define the sequence of beth cardinals by
and
for
a limit ordinal. Then the strong limit cardinals are precisely the
with
or a limit ordinal.
Theorem 9. (Bukovský-Hechler).
- If
is infinite then
- In particular, if
is strong limit, then
- Let
be singular, and assume that the exponential
is eventually constant below
; i.e., there is some
and some
such that for all cardinals
with
one has
Then also
The theorem illustrates that the exponential map must satisfy certain restrictions, at least on its values on the singular cardinals. It is well known since the beginnings of forcing, from the work of Easton, that the exponential is `essentially’ arbitrary on the regular cardinals except that, of course, it is monotonic: If then
and must obey König’s lemma,
However, once large cardinals are considered, these are not the only restrictions. We will show this in Section 4.
Proof. 1. Let be infinite and let
Let
be strictly increasing, and let
for all
so
Then
as the obvious bijection verifies. But
On the other hand, clearly
for all
so
and therefore
The result follows from these two inequalities.
2. If is strong limit and
is as above, then
On the other hand, for any
so
, and 2. follows from 1.
3. Assume is singular. With
as above, if
is sufficiently large,
. But then
, since we can take
The result follows from 1.
For example, if for all
(this situation is easily achieved by forcing) then also
The next result provides an easy `algorithm’ to compute any power, provided we know the values of the exponential function, the cofinality map, and the gimel function I’ll expand on this remark after the proof of the theorem.
Theorem 10. Let and
be infinite cardinals. Let
Then
Proof. 1. If then
2. If then any function
is bounded, so
and
3. Suppose that
and
is eventually constant (and equal to
) as
approaches
Since
is a singular cardinal and we can choose a strictly increasing sequence of cardinals
cofinal in
such that
for all
In particular,
.
Note that for each
so also
[Of course, it follows from König’s lemma that in fact we have a strict inequality, but we only need this weaker estimate.]
We now have The other inequality is clear.
4. Finally, suppose that
and
is not eventually constant as
approaches
Notice that if then
Otherwise,
for any
, and the map
would be eventually constant below
after all. Hence,
Choose an increasing sequence of cardinals cofinal in
Then
The other inequality is clear.
Remark. By induction, it follows from Theorem 10 that the computation of the function `reduces’ to computations of the functions
and
for
a cardinal, and the function
for
an ordinal. More precisely, if
and
are two models of set theory (with choice) with the same ordinals, and the values of any of these three functions are the same whether they are computed in
or in
, then also all the powers
are the same, whether they are computed in
or in
Forcing has shown that there is not much one can say about the exponential function when restricted to successor cardinals and small large cardinals. This indicates that to understand cardinal arithmetic, one’s efforts must concentrate on the exponential function on singular and large cardinals, and on the gimel function.
In fact, the gimel function suffices to compute the exponential by Theorem 9: First,
for
regular. Assume now that
is singular. Let
If
is not eventually constant below
then clearly
, and
by Theorem 9.1, while if
is eventually constant below
then
by Theorem 9.3.
This observation explains why the bulk of research in cardinal arithmetic concentrates on understanding the gimel function. As we will see next time, this naturally leads to the study of certain infinite products. This latter study has proved quite fruitful. We will study two outcomes: Silver’s theorem, and one of the Galvin-Hajnal results. Then, we will briefly mention how Shelah has extended and generalized these theorems with his development of pcf theory.
Thank you so much professor Caicedo for these online classes.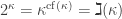 (the formula right after “by theorem 9”).
(the formula right after “by theorem 9”).
In the paragraph right before the last one, I think you meant to write (if I am not mistaken)
Hi, and second,
and second,  (trivially) if
(trivially) if  is regular, in which case it then just happens that
is regular, in which case it then just happens that 
What I meant is: First,
There was a typo at the end of that paragraph, though; the second “is not eventually constant” should have been “is eventually constant.” It is now fixed.
Oh I see, indeed is a regular cardinal so we can write
is a regular cardinal so we can write  Thank you professor Caicedo.
Thank you professor Caicedo.
I don’t want to take to much of your time but I would like to mention a theorem in Jech’s Set Theory whose demonstration seems quite hard to understand. It is Pospisil Theorem in page 75 which states that for every infinite cardinal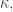 there exist
there exist 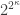 uniform ultrafilters on
uniform ultrafilters on 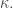 First Jech proves a lemma stating that there exists an independent family of subsets of
First Jech proves a lemma stating that there exists an independent family of subsets of  of cardinality
of cardinality 
 of subsets of
of subsets of  is independent if for any distinct
is independent if for any distinct  the intersection
the intersection
 has cardinality
has cardinality 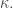
He defines an independent family: a family
Now in the proof of Pospisil’s theorem, Jech states: Let be an independent family of subsets of
be an independent family of subsets of 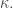
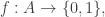 consider this family of subsets of
consider this family of subsets of  :
:
 This family is independent and thus has the finite intersection property (he does this to prove that this family is included in an ultrafilter because thx to a previous lemma if a family has the finite intersection property then it is included in a filter, and then we extend it to an ultrafilter).
This family is independent and thus has the finite intersection property (he does this to prove that this family is included in an ultrafilter because thx to a previous lemma if a family has the finite intersection property then it is included in a filter, and then we extend it to an ultrafilter).
For every function
The problem is that I can’t see why this family independent and has the finite intersection property.
Any hint?
Thank you.
[…] the end of last lecture we showed Theorem 10, a general result that allows us to compute products for infinite cardinals […]
Hi hurburble,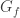 is independent. This is false, just look at sets in the first of the three members of the union that make up
is independent. This is false, just look at sets in the first of the three members of the union that make up  What you want is that
What you want is that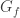 has the finite intersection property. This is easy since
has the finite intersection property. This is easy since  is independent. I’ll let you think about it on your own.
is independent. I’ll let you think about it on your own.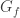 is uniform. This is easy from the sets in the first of the three members of the union that make up
is uniform. This is easy from the sets in the first of the three members of the union that make up 
 then
then  does not have the finite intersection property. You want this to guarantee that any ultrafilter extending
does not have the finite intersection property. You want this to guarantee that any ultrafilter extending 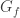 is different from any ultrafilter extending
is different from any ultrafilter extending  This is easy from the fact that if
This is easy from the fact that if  then for some
then for some 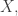
 but
but 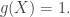
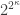 many functions
many functions  so there are at least that many collections
so there are at least that many collections 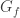 and therefore at least that many ultrafilters. This is easy from the size of
and therefore at least that many ultrafilters. This is easy from the size of 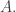
I don’t think you need (or want) to prove that
1.
2. Any ultrafilter extending
3. If
4. There are at least
Hi Mr Caicedo,
Thank you so much for your explanation
1) Indeed, you are right,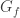 is not independent, it is
is not independent, it is  which is independent.
which is independent.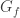 has the finite intersection property.
has the finite intersection property. is independent then none of its elements can be the null set. If none of the elements of this family can be the null set then
is independent then none of its elements can be the null set. If none of the elements of this family can be the null set then 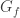 has the finite intersection property because none of the elements of
has the finite intersection property because none of the elements of 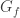 can be the null set since
can be the null set since 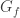 is constructed with the help of elements of
is constructed with the help of elements of 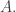 In other words the elements of
In other words the elements of 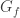 are pairwise disjoint.
are pairwise disjoint.
I think I figured out why
if
2)Any ultrafilter extending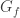 is uniform because for all
is uniform because for all  the cardinality of
the cardinality of  is
is 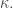
3) I now see why we don’t want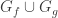 to have the finite intersection property. It is to guarantee that we have distinct ultrafilters in the end.
to have the finite intersection property. It is to guarantee that we have distinct ultrafilters in the end.
4) Indeed, the cardinality of is
is 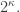
Again, thank you!
Hi again,
One last pass at it:
1) What you say is not enough to guarantee that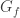 has the finite intersection property. I also assume at the end you meant “not pairwise disjoint,” but what you say does not imply this. You actually need to use the fact that
has the finite intersection property. I also assume at the end you meant “not pairwise disjoint,” but what you say does not imply this. You actually need to use the fact that  is independent, and the way that
is independent, and the way that 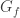 is defined.
is defined.
2) What you say is not enough. You need to use the way that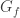 is defined.
is defined.
3) and 4) are fine.
Hi again,
1) Except for the fact that any finite subset of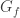 has nonempty intersection because
has nonempty intersection because 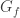 is constructed with elements of
is constructed with elements of 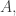 I am not able to find another argument to make it accurate.
I am not able to find another argument to make it accurate.
2) It seems to me that the sets that make up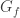 are large enough as to have an impact on the cardinality of the set resulting from taking them out of
are large enough as to have an impact on the cardinality of the set resulting from taking them out of 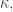 which means that they have infinite cardinality cofinal in
which means that they have infinite cardinality cofinal in 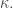 Except from that argument, I can’t see the full justification.
Except from that argument, I can’t see the full justification.
I think the source of all my trouble comes from me being in difficulty understanding the way an independent family is defined.
is defined.
It seems to me that in order for the condition to be fulfiled (i.e. for the intersection to have cardinality ) we need to choose the sets
) we need to choose the sets 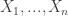 large enough, with a cardinality
large enough, with a cardinality  and the sets
and the sets  small enough (with a cardinality that can’t be mapped cofinally in
small enough (with a cardinality that can’t be mapped cofinally in  ) so we can end up with an intersection of cardinality
) so we can end up with an intersection of cardinality 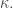
Does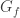 has the finite intersection property because it is a filter (it looks like a principal filter because of the condition
has the finite intersection property because it is a filter (it looks like a principal filter because of the condition  ) and it is filter because of
) and it is filter because of  being independent?
being independent?
I am afraid that’s all I can make out of all of this.
[…] any power can be computed from the cofinality and gimel functions (see the Remark at the end of lecture II.2). What we can say about the numbers varies greatly depending on whether is regular or not. If is […]
[…] Before stating Silver’s result, we need one additional result. Recall that was introduced last lecture in Definition 4, it is the statement that for all infinite cardinals We break the result into two parts, Lemmas 17 and 18, corresponding respectively to Theorems II.1.9 (describing the behavior of the exponential ) and II.1.10 (describing the computation of powers ) from lecture II.2. […]
[…] This follows from Corollary 4: If , then by Theorem II.1.10 from lecture 2. But so both and are strictly smaller than […]
[…] 2, recall from Corollary 8 in lecture II.2 […]
[…] , then . I have addressed both these computations in my lecture notes for Topics in Set Theory, see here and […]
[…] , then . I have addressed both these computations in my lecture notes for Topics in Set Theory, see here and […]
[…] any power can be computed from the cofinality and gimel functions (see the Remark at the end of lecture II.2). What we can say about the numbers varies greatly depending on whether is regular or not. If is […]
[…] 2, recall from Corollary 8 in lecture II.2 […]