414/514 – The Schoenberg functions

Here is Jeremy Ryder’s project from last term, on the Schoenberg functions. Here we have a space-filling continuous map whose coordinate functions and are nowhere differentiable.

The proof that are continuous uses the usual strategy, as the functions are given by a series to which Weierstrass -test applies.

The proof that is space filling is nice and short. The original argument can be downloaded here. A nice graph of the first few stages of the infinite fractal-like process that leads to the graph of can be seen in page 49 of Thim’s master thesis.

414/514 – Faber functions

Here is Shehzad Ahmed’s project from last term, on the Faber functions, a family of examples of continuous nowhere differentiable functions. Ahmed’s project centers on one of them, but the argument can be easily adapted to all the functions in the family.

As usual, the function is given as a series where the functions 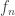are continuous, and we can find bounds 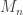with and . By the Weierstrass -test, is continuous. Also, the strategy for nowhere differentiability is typical: We associate with each point a pair of sequences and with 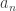strictly decreasing to and 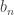strictly increasing to . The key lemma (shown, for example, in Johan Thim’s Master thesis available here) is that, if a continuous function is differentiable at , then we have

In the case of the Faber functions, the functions 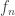add `peaks’ in the neighborhood of any point, and the locations of these peaks can be used as the points 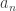and 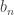; moreover, the slopes accumulate at these peaks, and so the limit on the right hand side of the displayed equation above does not converge and, in fact, diverges to 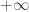or .

Faber’s original paper, Einfaches Beispiel einer stetigen nirgends differentiierbaren Funktion, Jahresbericht der Deutschen Mathematiker-Vereinigung, (1892) 538-540, is nice to read as well. It is available through the wonderful GDZ, the Göttinger Digitalisierungszentrum.

414/514 – Katsuura function

Here is Erron Kearns’s project from last term, on the Katsuura function, an example of a continuous nowhere differentiable function.

The presentation is nice: As usual with these functions, this one is defined as the limit of an iterative process, but the presentation makes it very clear the function is a uniform limit of continuous (piecewise linear) functions, and also provides us with a clear strategy to establish nowhere differentiability.

Actually, the function is presented in a similar spirit to many fractal constructions, where we start with a compact set and some continuous transformations . This provides us with a sequence of compact sets, where we set and . Under reasonable conditions, there are several natural ways of making sense of the limit of this sequence, which is again a compact set, call it , and satisfies , i.e., is a fixed point of a natural “continuous” operation on compact sets.

This same idea is used here, to define the Katsuura function, and its fractal-like properties can then be seen as the reason why it is nowhere differentiable.