Quite a few of you had difficulties with problem 18 of the Additional and Advanced Exercises for Chapter 10, so I am posting a solution here.
The problem asks to derive the trigonometric identity  by forming the cross product of two appropriate vectors.
by forming the cross product of two appropriate vectors.
In problems that involve trigonometry or geometry, it is convenient to begin with vectors that have some clear geometric meaning related to the problem at hand, so it seems natural to consider the vectors  and
and  .
.
These are two vectors in the plane, but we look at them as vectors in 3-D, as we should, since we want to look at their cross product, and this is only defined for vectors in 3-D.
So: 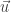 is a vector of size 1 (
is a vector of size 1 ( ) that forms an angle of
) that forms an angle of  radians with the
radians with the  -axis (measured counterclockwise). Similarly,
-axis (measured counterclockwise). Similarly,  is a vector of size 1 that forms an angle of
is a vector of size 1 that forms an angle of  radians with the
radians with the  -axis (measured counterclockwise).
-axis (measured counterclockwise).
Now: We need to analyze the angle between 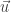 and
and  , which seems to be the technical point of this exercise, so let’s do this very carefully. This angle is the angle measured starting at
, which seems to be the technical point of this exercise, so let’s do this very carefully. This angle is the angle measured starting at 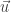 and moving counterclockwise until we find
and moving counterclockwise until we find  , is usually
, is usually 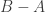 , but it may be
, but it may be 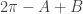 if, for example,
if, for example, 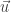 and
and  are vectors in the first quadrant and
are vectors in the first quadrant and  . (Although we can “ignore” this case since the sine function is periodic with period
. (Although we can “ignore” this case since the sine function is periodic with period 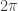 .)
.)
Similarly: The direction of  is obtained by the Right-Hand Rule, meaning
is obtained by the Right-Hand Rule, meaning  is a vector perpendicular to the plane spanned by
is a vector perpendicular to the plane spanned by 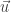 and
and  (the
(the  -plane), but it may be a positive (or zero) multiple of
-plane), but it may be a positive (or zero) multiple of  , or a negative multiple of
, or a negative multiple of  , depending on whether the angle between
, depending on whether the angle between 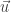 and
and  is smaller than (or equal to)
is smaller than (or equal to)  , or larger than
, or larger than  .
.
The magnitude of  is
is 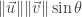 , where
, where  is either the angle
is either the angle  between
between 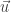 and
and  , or
, or 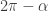 , whichever is between
, whichever is between 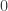 and
and 
Putting these two bits of information (about direction and magnitude) together, we find that  if
if 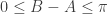 . If
. If  , then
, then 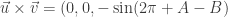 but
but  for any
for any  , so also in this case
, so also in this case  .
.
Finally,  , component-wise, is found by computing the formal determinant
, component-wise, is found by computing the formal determinant  . Comparing this expression with the one above, we find the desired identity.
. Comparing this expression with the one above, we find the desired identity.
(Actually, we find it with the roles of  and
and  reversed, but this is of course irrelevant. And of course this deduction only works for angles between
reversed, but this is of course irrelevant. And of course this deduction only works for angles between 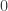 and
and 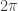 , but the identity is true in all other cases as well, thanks to the periodicity properties of sine and cosine.)
, but the identity is true in all other cases as well, thanks to the periodicity properties of sine and cosine.)



 Posted by andrescaicedo
Posted by andrescaicedo