In this set of notes I want to sketch Gödel’s proof that is consistent with the other axioms of set theory. Gödel’s argument goes well beyond this result; his identification of the class
of constructible sets eventually led to the development of inner model theory, one of the main areas of active research within set theory nowadays.
A good additional reference for the material in these notes is Constructibility by Keith Devlin.
1. Definability
The idea behind the constructible universe is to only allow those sets that one must necessarily include. In effect, we are trying to find the smallest possible transitive class model of set theory.
is defined as
where
for
limit, and
where
The first question that comes to mind is whether this definition even makes sense. In order to formalize this, we need to begin by coding a bit of logic inside set theory. The recursive constructions that we did at the beginning of the term now prove useful.
I won’t provide full details, but I expect that what follows allows you to fill in the gaps without difficulties.We begin by coding formulas inside set theory. For this, we begin by coding variables. What I mean is, recall that our official list of variables is even though we usually write
We need to assign a set to each variable in a way that whenever we want to talk about the variable, we can instead talk about the set. Then we will do the same for all the logical symbols, and use this to code formulas.
One simple way of coding variables is letting the ordered pair code the variable
Clearly, there is a formula
that holds of iff
codes a variable, namely,
states that
is an ordered pair, that its first coordinate is 0, and its second coordinate is a natural number.
(Later, we will code some symbols with natural numbers. It is in order to distinguish between these symbols and the variables, that we use rather than simply
to code
)
It will prove convenient to use constants, to represent sets. We have a constant for each set
. We want to code each constant by a set. One way could be to simply let the set
act as the constant
Unfortunately, this would be ambiguous, as when we have coded a formula
by a set
, we wouldn’t know whether
is coding
or the constant
, for example. There are other issues as well. For this reason, we choose to code the constant
by the ordered pair
As before, there is a formula
which holds of iff
codes a constant
for some
Now that we have coded variables and constants, we can code formulas. We will represent the logical symbols as follows:
and other symbols, are treated as abbreviations.
We begin by coding atomic formulas. Remember that these are formulas of the form or
where
are either constants or variables. We simply code them by a finite sequence and, in general, we will use finite sequences to represent formulas. The sequence coding
where
is either
or
would be
where
codes
,
codes
,
codes
, etc. Formally, we see that there is a formula
That holds iff codes an atomic formula:
says that
is a function with domain
that
and, for
To code arbitrary formulas, remember that to each we can associate a parsing sequence
consisting of the subformulas of
listed in such a way that whenever a formula
is listed, all its subformulas have been listed before, and that if
appears in a parsing sequence, then it is indeed a formula. We can then define
by saying that there is a function with domain some natural number
and such that
and, for all
we have that
or there is a such that
where is the formula coded by
(which we can take simply to mean that
is a sequence of length
that
and
), or there are
such that
where are the formulas coded by
(meaning,
is a sequence of length 5,
and
), or there is
, and a variable
such that
where is the formula coded by
(meaning,
is a sequence of length 3,
and
). Any function
witnessing
we can call a parsing witness for
We can then define a class function
that, whenever holds, assigns to
the set of free variables of the formula
coded by
Remember that this means that
is a formula of two free variables, that for every
there is a unique
such that
holds, and that if
, then
is as stated and, as usual, we write
rather than
The definition of
is by recursion, using a parsing witness for
. More carefully, we define
by recursion, so that if
fails, then
Otherwise,
- If
codes
then
is
if exactly one of
is a variable, and that variable is
or
if
and
or
otherwise.
- If
codes
and
codes
then
I.e., if
and
is a formula, then
- If
codes
and
code
then
- If
codes
and
codes
then
In order to do this, we use a parsing witness for
One checks that, no matter what parsing witness is used,
is always computed the same way.
We can then define a formula describing satisfiability. This is a formula
which holds iff codes a formula in the language of set theory
(i.e.,
is the only non-logical symbol in
, and the free variables of
are exactly as shown),
is a tuple of elements of
,
and, letting
be the formula resulting from substituting in
each free occurrence of
by
we have
(We may also write or even the admittedly ambguous
for
)
This definition is by recursion on the complexity of of course. More precisely, the definition refers to a parsing witness for
and implements the inductive clauses of Tarski’s definition of truth in models. As before, there ends up being no difference, no matter what parsing witness is used. I omit additional details, but it should be routine at this point to write down in detail both the formula
and the formula
The point of all this is that, now that we have a single formula which captures the notion of satisfiability, then we can define
by
Note that now that we have a formula describing it follows that “
” is also expressible by a formula, i.e.,
is indeed a class. Clearly, then, if
is a set, then so is
as
and this is a set, by comprehension.
Remark 1 We have taken advantage in this section of the fact that in set theory, we can directly use functions. Gödel’s incompleteness theorem for Peano Arithmetic begins in very much the same form, by coding logic inside number theory. But Gödel has the additional problem that, in number theory, we do not have functions but only numbers, and so he first needs to device a way of coding finite sequences by numbers.
Once this is done, there is still the problem that there does not seem to be a reasonable way of coding arbitrary models by numbers, so instead Gödel works not with satisfiability but with provability. The possibility of using models directly is another advantage of working within set theory.
Remark 2 On the other hand, although we have a formula
that we can use to code all statements of the form
for
a set and
a formula, we do not have a formula
that holds of
iff
codes a formula that is true in
This is a somewhat subtle point related to both a theorem of Tarski usually called “undefinability of truth” and to Gödel’s incompleteness theorem.
Although I won’t prove this fact, informally, the issue is that expanding the definition of
for a formula
with
alternations of quantifiers requires itself
alternations, so there is no formula that (provably in
) works for all
And this is, ultimately, because
is a proper class rather than a set.
2. Basic properties of
In this section we present some basic properties of and of the constructible hierarchy
that we will require in the proof that
The basic facts listed in the theorem below, and the fact that
is a model of
.
- For all
we have
- For all
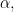
is transitive. Therefore,
is transitive.
- For all
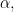
If
then
On the other hand, if
is infinite,
- Whenever
then
- For all
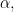
In particular,
contains all the ordinals.
Proof: We begin by arguing simultaneously by induction that, for all
is transitive and
for all
This is clear from the definition if is
and from the definition and induction, if
is a limit ordinal. Suppose now the result for
and argue for
For this, note that (by induction) it suffices to show that
and that
is transitive.
Let Then
since
is transitive. But then
This proves that
Now, if then
so
and, therefore,
This shows that
is transitive.
Now we show that for all
by induction. Again, this is immediate from the definitions if
is 0 or a limit ordinal. At successor ordinals, we have
We argue by induction that if
This immediately gives as well that
Suppose, then, that
(this clearly holds for
). Let
Then
say
a finite set, since itself is finite. But then
This shows that and we already have the other containment.
On the other hand, if for
infinite, then
where the first equality follows from noting that each element of is determined by a formula in the language of set theory (and there are only countably many of them) and a finite tuple of elements of
At limit stages we have that
where the sum indicates the size of a (possibly infinite) disjoint union.
We still need to check that for
infinite. This is a consequence of the next item, that
if
This is because, in particular, it follows that
and then of course
To prove the result, we only need to argue that The rest follows by induction. But
By induction, we have and a further inductive argument (looking for the least counterexample) gives that, in fact,
But then
That follows immediately, and this completes the proof.
Before we prove that we need a particular case of the reflection theorem:
Lemma 2 Suppose that
is a formula. Then there are arbitrarily large ordinals
such that
for all tuples

In the situation of the lemma, we say that is reflected down from
to
.
Proof: This can be established by an argument very similar to the one we used in the notes on the Löwenheim-Sk\o lem theorem. Namely, for and each of its subformulas
consider Sk\o lem functions
from
Let
be the set of these Sk\o lem functions. Recall that if
is closed under
then for any
we have that
iff
Now, given any we describe an iterative procedure: Let
be the closure of
under
Let
be least such that
In general, given
consider its closure
under
and let
be least such that
Now note that if
then
is closed under and therefore
has the required property. Since
was arbitrary, we are done.
We are now ready for the main result of this section:
Theorem 3 (Gödel)
Proof: Extensionality: This follows from transitivity of and extensionality in
Pairing: If then they belong to some
Then
Union: If let
be such that
Then
is definable in
Infinity:
Foundation: This follows from transitivity of and foundation in
Given
there is in
a
with
Since
is transitive,
Power set: Given we can let
Note that is a set, as it is the range of a function
Let
and
Then and
i.e.,
Note there is no reason to suspect that is actually the true
Comprehension: Let let
be a formula, and let
be a tuple of elements of
Write
for the tuple of constants
for
in
Let
We need to show that It is here that Lemma 2 is useful: Pick
large enough so
and for any
iff
Then
Replacement: Let be a formula and let
be a tuple of sets in
such that
Let We need to find a
such that
since replacement for then follows by comprehension. Using replacement in
, let
the unique
such that
first appears in
Then
and we are done.
Choice: Note that since is a model of
the formalization of logic inside set theory can be carried out in
It then makes sense to talk, for any
of
i.e., the set that in
satisfies the definition of
One can easily verify by induction the following two claims:
- For all
- For all
To prove that choice holds in begin by fixing some sufficiently definable enumeration
of all (codes for) formulas without constant symbols (so the enumeration is in
). Given
let:
-
be the least
such that
-
be the least natural
such that
is definable over
using
and some parameters.
We now define with the properties that
is a well-ordering of
for all
and the orders end-extend each other, i.e,
and if
and
then
The construction is carried out inside
Once this is done, we can then define a global well-ordering of all of
by setting, for
iff either or else
say, and
The definition of the orderings is carried out by recursion in
and if
is limit,
Finally, given
we define
as follows: Given
set
iff
- Either
or else
-
but
or
-
and
but the tuple of parameters in
used to define
by means of the formula
precedes the corresponding tuple for
in the lexicographic ordering of tuples induced by
It is straightforward to check that the orderings so defined are indeed well-orderings, and we are done.
Remark 3 One can organize the proof of Comprehension in
somewhat more carefully, to avoid the appeal to the axiom of choice implicit in the use of Sk\o lem functions in the proof of Lemma 2. Note that the argument above can then be formalized in
since the proof that choice itself holds in
does not use the axiom of choice in
This establishes Gödel’s result that, if
is consistent, then so is
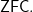
3. The condensation lemma
In this section we sketch the fundamental condensation lemma, the last preliminary result needed in the proof of in
The condensation lemma is in turn a consequence of the following basic result:
Lemma 4 (Mostowski collapsing lemma) If
is a set and
satisfies the axiom of extensionality, then there is a unique transitive set
and a unique map
that is an isomorphism between
and
Moreover,
is the identity on any transitive subset of
Proof: Suppose that is as wanted. Then, for any
with
we have
Also, if
then there must be some
such that
and we have
This means that
By induction on the rank of it follows that there is a unique map
defined by recursion by means of the equation above. Letting
be the range of
it also follows that
is unique.
By extensionality, it is routine to check that so defined is injective, and therefore a bijection between
and
In effect, suppose
is of least rank such that there is some
distinct from
and such that
If there is some then, by definition of
we have
so (by definition of
again) we must have
with
Since
we have
But then
contradicts the minimality of the rank of
A similar contradiction is obtained if
By definition of as the range of
we have that
is indeed transitive. It remains to verify that
is an
-isomorphism. By definition,
for
implies
Suppose now that
and
Since
is injective, it follows that
and we are done.
That is the identity for any
that is already transitive is now immediate.
is usually called the collapsing map, and
is the collapse of
The condensation lemma extends the above when is an elementary substructure of an initial segment of
by concluding that the transitive set
it collapses to, is also an initial segment of
Theorem 5 (Condensation lemma) Suppose
is a limit ordinal, and
i.e.,
is an elementary substructure of
Then there is a unique
and a unique map
such that
is an isomorphism.
Proof: Begin by checking that To do this, argue by induction on
that
for all
since every element of
is definable. In particular, if
there is nothing to prove. Now suppose
Note that satisfies the axiom of extensionality, and therefore so does
The existence and uniqueness of
now follows from Mostowski’s collapsing lemma. Let
be the collapsing map.
We want to show that for some
But this follows from checking that the construction of
can be carried out inside
with
being the output. Hence,
i.e.,
Then and one checks that
for all
It follows that
Since each ordinal of
is
for some ordinal
it is clear that
4. holds in
We conclude the course by showing:
Theorem 6 (Gödel)
Proof: We argue inside (or, if you wish, within the theory
). Let
be a cardinal, and let
be a subset of
There is some
such that
and it suffices to show that the least such
is strictly smaller than
Because then
and this set has size
by Theorem 1.
To see this, let be large enough and a limit ordinal, so that
Let
be an elementary substructure of
of size
and such that
Let
be the transitive collapse of
and let
be the collapsing map. Note that
as
and
is the identity on
since
is transitive and
Since
has size
so does
so
has size
Since
we are done.
We have thus established that, if is consistent, then so is
In particular, this shows that one cannot refute
in
On the other hand, in 1963, Paul Cohen devised a very powerful method, known as forcing that, in particular, can be used to show that if
is consistent, then so are
and
This provides a concrete example of a natural mathematical statement (namely,
) verifying the incompleteness theorem for set theory.
Typeset using LaTeX2WP. Here is a printable version of this post.
[Edited Dec. 11]
Here I sketch two suggestions for how to avoid appealing to Choice in the proof of the reflection argument:
1. Prove choice in first. This require a bit of care, checking that (without appealing to replacement or comprehension) inside
first. This require a bit of care, checking that (without appealing to replacement or comprehension) inside  we can organize the proof I presented here. Once this is done, we can define in
we can organize the proof I presented here. Once this is done, we can define in  the Skølem functions we need for the reflection argument. This is fine but it is technically somewhat demanding.
the Skølem functions we need for the reflection argument. This is fine but it is technically somewhat demanding.
Or we could do as follows, which is easier and feels like the natural approach:
2. Check that one can prove the reflection theorem without appealing to choice. Previously, given a structure and a formula
and a formula  we defined the Skølem function
we defined the Skølem function  by saying that
by saying that  is the least
is the least  such that
such that 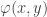 holds in
holds in  if there is some such
if there is some such 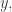 and as a previously fixed element of
and as a previously fixed element of  otherwise. (Where “least” is with respect to a fixed well-ordering of
otherwise. (Where “least” is with respect to a fixed well-ordering of 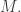 ) In
) In 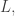 we can eliminate the use of choice by being somewhat less careful: Now let
we can eliminate the use of choice by being somewhat less careful: Now let  be the set of
be the set of  such that
such that 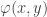 holds in
holds in 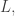 where
where  is least such that, if there is some
is least such that, if there is some  such that
such that  then there is some such
then there is some such  in
in 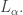 The difference is that rather than picking a single witness
The difference is that rather than picking a single witness 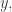 we are now potentially picking a very large set of witnesses. Of course, if
we are now potentially picking a very large set of witnesses. Of course, if  is closed under
is closed under  then if
then if 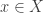 and
and  then there is a
then there is a  such that
such that  With this definition, we can now proceed as before.
With this definition, we can now proceed as before.
The (new) notion of being closed is the natural one: is closed under
is closed under  iff for any
iff for any 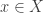 we have
we have 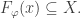
[Comment migrated to the other site.]