580 -Cardinal arithmetic (11)

March 12, 2009

4. Strongly compact cardinals and {{\sf SCH}}

 

Definition 1 A cardinal {\kappa} is strongly compact iff it is uncountable, and any {\kappa}-complete filter (over any set {I}) can be extended to a {\kappa}-complete ultrafilter over {I.}

 

The notion of strong compactness has its origin in infinitary logic, and was formulated by Tarski as a natural generalization of the compactness of first order logic. Many distinct characterizations have been found.

Read the rest of this entry »

1 Comment | 580: Topics in set theory | Tagged: , , , , , , , , , , , | Permalink
Posted by andrescaicedo

Set theory seminar -Forcing axioms and inner models VII

October 24, 2008

I concluded my series of talks by showing the following theorem of Viale:

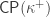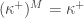Theorem (Viale). Assume {\sf CP}(\kappa^+) and let M\subseteq V be an inner model where \kappa is regular and such that (\kappa^+)^M=\kappa^+. Then {\rm cf}(\kappa)\ne\omega.

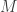This allows us to conclude, via the results shown last time, that if {\sf PFA} holds in V and M computes cardinals correctly, then it also computes correctly ordinals of cofinality \omega.

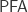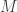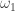An elaboration of this argument is expected to show that, at least  if we strengthen the assumption of {\sf PFA} to {\sf MM}, then M computes correctly ordinals of cofinality \omega_1. 

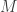Under an additional assumption, Viale has shown this:  If {\sf MM} holds in V, \kappa is a strong limit cardinal, (\kappa^+)^M=\kappa^+, and in M we have that \kappa is regular, then in V, the cofinality of \kappa cannot be \omega_1. The new assumption on \kappa allows us to use a result of Dzamonja and Shelah, On squares, outside guessing of clubs and I_{<f} [\lambda], Fund. Math. 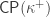148 (1995), 165-198, in place of the structure imposed by {\sf CP}(\kappa^+). It is still open if the corresponding covering statement 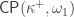{\sf CP}(\kappa^+,\omega_1) follows from {\sf MM}, which would eliminate the need for this the strong limit requirement.

  • Go to the intermezzo for a discussion of consistency strengths.

2 Comments | Set theory seminar | Tagged: , , | Permalink
Posted by andrescaicedo

Set theory seminar -Forcing axioms and inner models VI

October 17, 2008

I presented a sketch of a nice proof due to Todorcevic that {\sf PFA} implies the P-ideal dichotomy {\sf PID}. I then introduced Viale’s covering property {\sf CP} and showed that it follows from {\sf PID}. Next time I will indicate how it can be used to provide a proof of part 1 of the following theorem:

Theorem (Viale). Assume M\subseteq V is an inner model.

  1. If {\sf PFA} holds in V and M computes cardinals correctly, then it also computes correctly ordinals of cofinality \omega.
  2. If {\sf MM} holds in V, \kappa is a strong limit cardinal, (\kappa^+)^M=\kappa^+, and in M we have that \kappa is regular, then in V, the cofinality of \kappa cannot be \omega_1. 

It follows from this result and the last theorem from last time that if V is a model of {\sf MM} and a forcing extension of an inner model M by a cardinal preserving forcing, then {\sf ORD}^{\omega_1}\subset M.

In fact, the argument from last time shows that we can weaken the assumption that V is a forcing extension to the assumption that for all \kappa there is a regular cardinal \lambda\ge\kappa such that  in M we have a partition S^\lambda_\omega=\sqcup_{\alpha<\kappa}S_\alpha where each S_\alpha is stationary in V. 

It is possible that this assumption actually follows from {\sf MM} in V. However, something is required for it: In Gitik, Neeman, Sinapova, A cardinal preserving extension making the set of points of countable V cofinality nonstationary, Archive for Mathematical Logic, vol. 46 (2007), 451-456, it is shown that (assuming large cardinals) one can find a (proper class) forcing extension of V that preserves cardinals, does not add reals, and (for some cardinal \kappa) the set of points of countable V-cofinality in \lambda is nonstationary for every regular \lambda\ge\kappa^+. Obviously, this situation is incompatible with {\sf PFA} in V, by Viale’s result.

2 Comments | Set theory seminar | Tagged: , , , | Permalink
Posted by andrescaicedo