305 -Fields (5)

February 27, 2009

At the end of last lecture we stated a theorem giving an easy characterization of subfields of a given field {\mathbb F}. We begin by proving this result.

Theorem 18. Suppose {\mathbb F} is a field and S\subseteq{\mathbb F}. If S satisfies the following 5 conditions, then S s a subfield of {\mathbb F}:

  1. S is closed under addition.
  2. S is closed under multiplication.
  3. -a\in S whenever a\in S.
  4. a^{-1}\in S whenever a\in S and a\ne0.
  5. S has at least two elements.

Read the rest of this entry »

2 Comments | 305: Abstract Algebra I | Tagged: , , , , | Permalink
Posted by andrescaicedo

305 -Fields (4)

February 20, 2009

Suppose that {\mathbb F} is a field and that S\subset{\mathbb F}. It may be that S is also a field, using the same operations of {\mathbb F}. For example, if {\mathbb F}={\mathbb R}, then we could have S={\mathbb Q}.

Definition 15. If {\mathbb F} is a field and S\subset{\mathbb F}, we say that S is a subfield of {\mathbb F} if S is a field with the operations of {\mathbb F}.

Read the rest of this entry »

1 Comment | 305: Abstract Algebra I | Tagged: | Permalink
Posted by andrescaicedo

305 -Fields (3)

February 18, 2009

At the end of last lecture we arrived at the question of whether every finite field is a {\mathbb Z}_p for some prime p.

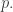
In this lecture we show that this is not the case, by exhibiting a field of 4 elements. We also find some general properties of finite fields. Finite fields have many interesting applications (in cryptography, for example), but we will not deal much with them as our focus through the course is on number fields, that we will begin discussing next lecture.

We begin by proving the following result:

Lemma 13. Suppose that 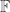{\mathbb F} is a finite field. Then there is some natural number 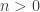n>0 such that the sum of n ones vanishes, 1+\dots+1=0. The least such n is a prime that divides the size of the field. 

Read the rest of this entry »

2 Comments | 305: Abstract Algebra I | Tagged: , | Permalink
Posted by andrescaicedo

305 -Fields (2)

February 13, 2009

We continue from last lecture. Examination of a few particular cases finally allows us to complete Example 6. The answer to whether {\mathbb Z}_n (with the operations and constants defined last time) is a field splits into three parts. The first is straightforward.

Lemma 10. For all positive integers n>1, {\mathbb Z}_n satisfies all the properties of fields except possible the existence of multiplicative inverses. \Box.

This reduces the question of whether {\mathbb Z}_n is a field to the problem of finding multiplicative inverses, which turns out to be related to properties of n.
Read the rest of this entry »

1 Comment | 305: Abstract Algebra I | Tagged: , | Permalink
Posted by andrescaicedo

305 -4. Fields.

February 11, 2009

Definition 1. Let {\mathbb F} be a set. We say that the quintuple ({\mathbb F},+,\times,0,1) is a field iff the following conditions hold:

  1. +:{\mathbb F}\times {\mathbb F}\to {\mathbb F}.
  2. \times:{\mathbb F}\times {\mathbb F}\to {\mathbb F.} (We say that {\mathbb F} is closed under addition and multiplication.)
  3. 0,1\in{\mathbb F}.
  4. 0\ne1.
  5. Properties 1–9 of the Theorem from last lecture hold with elements of {\mathbb F} in the place of complex numbers, {}0 in the place of \hat0, and {}1 in the place of \hat1.

Read the rest of this entry »

4 Comments | 305: Abstract Algebra I | Tagged: , | Permalink
Posted by andrescaicedo