305 -Fields (5)

February 27, 2009

At the end of last lecture we stated a theorem giving an easy characterization of subfields of a given field {\mathbb F}. We begin by proving this result.

Theorem 18. Suppose {\mathbb F} is a field and S\subseteq{\mathbb F}. If S satisfies the following 5 conditions, then S s a subfield of {\mathbb F}:

  1. S is closed under addition.
  2. S is closed under multiplication.
  3. -a\in S whenever a\in S.
  4. a^{-1}\in S whenever a\in S and a\ne0.
  5. S has at least two elements.

Read the rest of this entry »

2 Comments | 305: Abstract Algebra I | Tagged: , , , , | Permalink
Posted by andrescaicedo

175 -The sine integral

November 5, 2008

The integral \displaystyle\int_0^\infty\frac{\sin x}x\,dx is an example of an improper integral: The integrand is not defined at 0, and the interval of integration is unbounded. The issue at 0 is not really serious, since

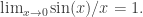
\lim_{x\to 0}\sin(x)/x=1.

Since the interval is unbounded, this integral is actually defined as a limit,

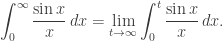
\displaystyle \int_0^\infty\frac{\sin x}x\,dx=\lim_{t\to\infty}\int_0^t\frac{\sin x}x\,dx.

In this post I want to show how to evaluate this limit. The problem is that the sine integral 

\displaystyle {\rm Si}(t)=\int_0^t \frac{\sin x}x\,dx

does not admit an elementary expression, i.e., it cannot be expressed in terms of t by composing exponentials, logarithms, trigonometric functions, their inverses, and polynomials.

(To get a sense of the difficulty in finding an expression for {\rm Si}(x), it may be useful to play a little trying integration by parts or similar tricks.)

 

Si(t)

This is a classical integral and appears in applications with some frequency, so there are several standard methods of computing its value. Usually, these methods involve techniques from complex analysis (either the Fourier transform or contour integrals), although there are some elementary approaches as well, such as the one I illustrate here. “Elementary” is to be taken with a grain of salt; although the argument below is easy to follow with some patience, it is difficult to come up with. There are good references where the integral is computed, but it usually takes me a while to remember where to look, so I decided to write this post and to provide a reference here as well.

An excellent book where the computation can be found more or less in complete detail (except for what I call Claims 1 and 2 below) is Introduction to Calculus and Analysis, vol. I, by Richard Courant and Fritz John, Interscience Publishers (1965), reprinted by  Springer (1989). The argument I present here is essentially the same they use, although I have arranged some of the details in a different way.

Read the rest of this entry »

1 Comment | 175: Calculus II | Tagged: , , , | Permalink
Posted by andrescaicedo