580 -Some choiceless results (5)

February 2, 2009

[This lecture was covered by Marion Scheepers. Many thanks! The notes below also cover lecture 6.]

We want to prove the following result and a few related facts.

Theorem. (Specker). {\rm CH}({\mathfrak m}) and {\rm CH}(2^{\mathfrak m}) imply 2^{\mathfrak m}=\aleph({\mathfrak m}).

It follows immediately from the theorem that {\sf GCH} implies {\sf AC}, since the result gives that any (infinite) {\mathfrak m} embeds into \aleph({\mathfrak m}).

Read the rest of this entry »

3 Comments | 580: Topics in set theory | Tagged: , , , | Permalink
Posted by andrescaicedo

580 -Some choiceless results (4)

January 29, 2009

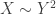Let me begin with a remark related to the question of whether \aleph(X)\preceq {\mathcal P}^2(X). We showed that this is the case if X\sim Y^2 for some Y, or if X is Dedekind-finite.

Theorem. The axiom of choice is equivalent to the statement that any Dedekind-infinite cardinal is a square.

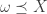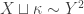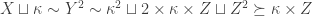Proof. Let X be a set. Assuming that every D-infinite cardinal is a square, we need to show that X is well-orderable. We may assume that \omega\preceq X. Otherwise, replace X with X\cup\omega. Let \kappa=\aleph(X). Assume that X\sqcup\kappa is a square, say X\sqcup\kappa\sim Y^2. Then \kappa\preceq Y^2. By Homework problem 2, \kappa\preceq Y, so Y\sim \kappa\sqcup Z for some Z, and X\sqcup \kappa\sim Y^2\sim\kappa^2\sqcup 2\times\kappa\times Z\sqcup Z^2\succeq\kappa\times Z.

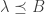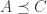Lemma. Suppose A,B,C are D-infinite sets and \lambda is an (infinite) initial ordinal. If \lambda\times A\preceq B\cup C then either \lambda\preceq B or A\preceq C.

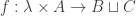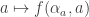Proof. Let f:\lambda\times A\to B\sqcup C be an injection. If there is some a\in A such that f(\cdot,a):\lambda\to B we are done, so we may assume that for all a\in A there is some \alpha\in\lambda such that f(\alpha,a)\in C. Letting \alpha_a be the least such \alpha, the map a\mapsto f(\alpha_a,a) is an injection of A into C. {\sf QED}

By the lemma, it must be that either \kappa\preceq X or else Z\preceq\kappa. The former is impossible since \kappa=\aleph(X), so Z is well-orderable, and thus so is Y, and since Y\sim Y^2\succeq X, then X is well-orderable as well. {\sf QED}

Read the rest of this entry »

1 Comment | 580: Topics in set theory | Tagged: , , , | Permalink
Posted by andrescaicedo