1. Introduction
Partition calculus is the area of set theory that deals with Ramsey theory; it is devoted to Ramsey’s theorem and its infinite and infinitary generalizations. This means both strengthenings of Ramsey’s theorem for sets of natural numbers (like the Carlson-Simpson or the Galvin-Prikry theorems characterizing the completely Ramsey sets in terms of the Baire property) and for larger cardinalities (like the -Rado theorem), as well as variations in which the homogeneous sets are required to possess additional structure (like the Baumgartner-Hajnal theorem).
Ramsey theory is a vast area and by necessity we won’t be able to cover (even summarily) all of it. There are many excellent references, depending on your particular interests. Here are but a few:
- Paul
András Hajnal, Attila Máté, Richard Rado, Combinatorial set theory: partition relations for cardinals, North-Holland, (1984).
- Ronald Graham, Bruce Rothschild, Joel Spencer, Ramsey theory, John Wiley & Sons, second edn., (1990).
- Neil Hindman, Dona Strauss, Algebra in the Stone-
compactification, De Gruyter, (1998).
- Stevo
High-dimensional Ramsey theory and Banach space geometry, in Ramsey methods in Analysis, Spiros Argyros, Stevo
Birkhäuser (2005), 121–257.
- András Hajnal, Jean Larson, Partition relations, in Handbook of set theory, Matthew Foreman, Akihiro Kanamori, eds., to appear.
I taught a course on Ramsey theory at Caltech a couple of years ago, and expect to post notes from it at some point. Here we will concentrate on infinitary combinatorics, but I will briefly mention a few finitary results.
In the early 1950s, Rado introduced the partition calculus notation, several variants of which we will be using through these lectures.
Definition 1 Let
be a set and
be a cardinal. Then
![{[X]^\tau=\{Y\subseteq X\colon|Y|=\tau\}.}](https://s0.wp.com/latex.php?latex=%7B%5BX%5D%5E%5Ctau%3D%5C%7BY%5Csubseteq+X%5Ccolon%7CY%7C%3D%5Ctau%5C%7D.%7D&bg=ffffff&fg=000000&s=0&c=20201002)
Let
be a cardinal. A function
is referred to as a
-partition or
-coloring of
. Sometimes one writes the partition “explicitly” as
where

Let
be cardinals, and let
be a sequence of cardinals. The arrow notation is defined as follows:
iff for any set
of size
and any coloring
there is an
and a set
such that
Here,
denotes the pointwise image of the set
under the function
We say that
is monochromatic, or homogeneous or
-homogeneous for the coloring
and also say that
admits an
-homogeneous subset of
of the prescribed size
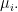
One reads
as arrows. The negation of the relation above is denoted by replacing
with

Although we are mostly interested in the version above, we will also consider the following:
Definition 2 An order type is an equivalence class of the collection of partial orders under the relation of order isomorphism; we denote the order type of a poset
by

When talking about order types of partially ordered sets, by
we mean the order type of
and by
we mean the order type of
The order type of an ordinal
is denoted also by
so the notation is consistent with the standard use for well-ordered sets.
If
is a partially ordered set and
is an order type, then
denotes
There is risk of ambiguity here, so when it matters we use
for the set of subsets of
of size
while
is used for the collection of subsets of (the partially ordered set)
of order type
If
are order types,
means that whenever
and
there is an order preserving injection (an embedding) of
into

If
denote order types,
is a cardinal, and
is a sequence of order types, then
iff for any poset
of order type
and any coloring
there is an
and a set
such that
As before, such an
is called homogeneous for

The notation is very flexible; if all the are equal to
one simply writes
and if
then one simply says
For example,
and
have the same meaning, and are true whether
denotes size or order type.
However daunting it appears at first sight, this notation is a very useful shorthand, and it compresses a large amount of information. We assume choice throughout unless otherwise stated; the results vary wildly in the absence of choice.
Note that if then
for any
and
such that
for all
2. The classical Ramsey’s theorem
Ramsey theory is to a large extent the study of the “arrow” relation, in a sense, a series of (vast) generalizations of the pigeonhole (or Schubfach-, or Dirichlet’s) principle.
The result that gave birth to the field is Frank Ramsey’s theorem from 1928, published in 1930, and obtained in order to show a decidability result.
Proof: The result is clear if by the pigeonhole principle.
We proceed by induction on Assume the result for
and let’s show it for
Let
be given. For
let
be the function
By induction define a sequence
as follows:
-
By induction, there is a number
and an infinite set
that is
-homogeneous for
- Inductively, let
There is then a
and an infinite
that is
-homogeneous for
Now consider the function given by
Let
be infinite and homogeneous for
Then the set
is infinite and homogeneous for
This proof has the advantage that it is easily finitizable. By this I mean, from the proof one can easily extract bounds that allow us to prove the following:
Proof: Argue by induction on We denote by
the least
as in the statement, and our task is to show that in fact
More generally, we let
be the smallest number
such that
so
To begin with, by the pigeonhole principle.
Given let
and define
for
by
for
The proof of Theorem 3 above easily shows that
One can see that, in fact, for all there is a constant
such that for all
where the tower of 2s has height
The case of Ramsey’s theorem has received special attention, the statement
being particularly well-known. Write
for
for
This is the smallest number
of vertices required to guarantee that whenever each edge of the complete graph
is colored either blue or red, there is either going to be a blue copy of
or a red copy of
Proof: The proof is by induction on Note that
Now argue that
from which the statement follows immediately.
To see the claimed inequality, consider a graph on many vertices, a coloring of its edges in colors blue and red, and let
be one of the vertices. Let
be the set of vertices that are joined to
by a blue edge and let
be the set of vertices joined to
by a red edge, so
It follows that either
or
Without loss, assume that It follows that either there is a red copy of
with vertices from
and we are done, or else, there is a blue copy of
with vertices from
In this case, all these vertices are joined to
by blue edges so, by adding
to them, we obtain a blue copy of
In fact, this was shown by Rödl. Very recently (in a paper to appear in the Annals of Mathematics), David Conlon has shown that for all
there is a constant
such that whenever
then
In joint work by David Conlon, Jacob Fox, and Benny Sudakov, the known bounds on have also been recently improved.
2.1. The happy end problem
The -Szekeres Theorem 5 above is responsible for popularizing Ramsey’s theorem.
and Szekeres reproved Ramsey’s result in 1934 when studying a question in elementary geometry, sometimes referred to as the “happy end problem.” (Another proof of Ramsey’s result had been found in 1933 by Skolem.)
Definition 6 For all natural numbers
let
denote the least
if it exists, such that given any
points in general position in the plane (i.e., no four of them lying on the same circle, no three of them being collinear, no two of the lines they determine being parallel), there are
that form the vertices of a convex
-gon.
For example, and
as observed by Esther Klein, who also asked the general problem of showing that
for all
is due to Makai, but the first published proof is due to J.D. Kalbfleisch, J.G. Kalbfleisch, and R. Stanton, in 1970.
To see that notice that 4 points do not suffice by considering the three vertices of a triangle and a fourth point inside. Now, given 5 points, consider their convex hull. We are done if it is not a triangle. If it is a triangle, there are two points inside, and the line
they determine does not cross one of the sides of the triangle. The quadrilateral with vertices these two points and the two vertices of the segment not crossed by
is convex.

Theorem 7 (
-Szekeres) For all
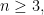
exists.
Shortly after their paper was published, Szekeres married Klein, which gave the name to the problem.
Proof: In fact, This is an argument of Michael Tarsy. As an undergraduate student at the Technion University, Tarsy was taking a combinatorics course under Lewin, and missed the lecture where the usual proof of the existence of
was presented so, when asked to in an exam, he produced the following instead:
Let and let
be
points in general position in the plane. For
color
blue if one encounters them in this order when going clockwise around the triangle they determine, and color them red otherwise.
One easily checks that four points determine a convex quadrilateral iff the set they form is homogeneous under the coloring just described, i.e., iff all its triples receive the same color. An easy induction shows that a set of points determines a convex
-gon iff any 4 of them determine a convex quadrilateral. The result follows.
The best known upper bound is shown by Tóth and Valtr in 1998. Shortly before, Bárány and Valtr showed that for any
there is a positive constant
such that any sufficiently large finite set
of points in the plane contains
subsets
each of size at least
such that every set
with
is in convex position.
It is conjectured that for all
That the right hand side is a lower bound is also due to
and Szekeres.
2.2. A decidability result
Ramsey proved his result to obtain an instance of the Entscheidungsproblem, a decidability theorem. Fix a first order language with no function symbols, and consider the formulas in the language, of the form
where is quantifier free. These are the so-called Bernays-Schönfinkel formulas.
Ramsey proved that there is an algorithm that decides whether these formulas have (finite) models. In contrast, it is well known (from results of Church and Trakhtenbrot) that the problem is undecidable for general first order formulas, and even for those of the form
with quantifier free.
Definition 8 Let
be a linearly ordered set. Let
Two sequences
and
of elements of
have the same ordering,
iff for all
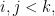
iff
Equivalently, if and
then
iff
The somewhat awkward definition allows for the possibility that two or more of the (and consequently, of the
) are the same.
Definition 9 A
-ary relation
on a linearly ordered set
is canonical on
iff whenever
then
For example, the canonical unary relations on a set are “true” (i.e.,
) and “false” (i.e.,
). The canonical binary relations are “false,” “
” “
” “
” “
” “
” “
,” and “true.”
Lemma 10 For all
there is
such that whenever
is
-colored for all
with
then there is an
such that
is monochromatic for all such
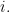
Proof: Let and for
let
Then we can take
Theorem 11 For all
there is
such that whenever
(whether finite or infinite), and
is a set of
many
-ary relations on
for all
with
then there is
on which all the relations in all the
are canonical.
Proof: This is a consequence of Lemma 10. Consider a cardinal and sets
of
-ary relations on
for
as in the statement of the theorem.
For define an equivalence relation on
by saying that whenever
, if
and
are the increasing enumerations of
and
respectively, then
iff the following holds: For all
with
all surjections
and all
For example, the equivalence class of a singleton is completely determined by the tuple of truth values of the relations
for
Clearly, there is an absolute (and easily computable) bound on the number of equivalence classes of these relations; “absolute” means here that
only depends on
and
but is independent of
and of the specific relations in
Now use Lemma 10 with the just described and
to find the required
noting that if
is monochromatic for the partition of
into equivalence classes for all
with
then all the relations in
are canonical on
Theorem 12 (Ramsey) Consider a language with only relation symbols, and let
be a finite theory all of whose axioms are universal, i.e., of the form
where
is quantifier free. There is a finite number
that only depends on the number
of variables, and the number and arity of the relations used in
such that for any
(whether finite or infinite), there is a model of
of size
iff there is a canonical model of
with universe
Here, we say that a model is canonical iff all the relations in its language are canonical.
Proof: Letting be the number of
-ary relations mentioned in
for
(for an appropriate
), we can take
as in Theorem 11.
First, if there is a model of
with universe
there is certainly a canonical substructure of
of size
since the language of
only has relation symbols. The universality of the axioms guarantees that this substructure is indeed a model of
Second, if there is a canonical model of
with universe
then there is one with universe any larger cardinal, obtained simply by extending each relation in the same canonical fashion. (For example, if a binary relation symbol
is interpreted in
by
then we also let
be its interpretation in any larger model.) That this extended structure is indeed a model of
follows easily from canonicity.
It is now relatively easy to extend the above result to give the decidability of the question of whether a Bernays-Schönfinkel sentence in a language with no function symbols is consistent. Essentially, one first replaces such a formula with a finite disjunction of universal formulas as above (in a possibly larger language).
Now, for any such formula take
and
as in the statement of Theorem 12, and note that whether or not
has a model of size
reduces to whether it has a canonical model with universe
There are only finitely many such models, so one can easily determine whether this is the case. If not, then one only has to examine the finitely many structures in the language of
of size less than
to see whether at least one of them models
Finally, whether the original formula is consistent or not is equivalent to whether our search was successful for at least one of the formulas in the disjunction
2.3. Tree arguments
It is convenient to examine other proofs of Ramsey’s Theorem 3, as they may illustrate different features than the argument above. Here is a proof that generalizes to the context of large cardinals; moreover, the technique it uses (trees and end-homogeneous sets) is widely applied in partition calculus. For the purpose of proving the argument is certainly more involved than the one we have given; on the other hand, it provides us with a fairly concrete (constructive) description of how to find homogeneous sets for given colorings:
Proof: The proof is by induction on For
the result is obvious.
The key to the inductive step is a mixture of König’s lemma and the construction of what now are called end-homogeneous sets. We first present the case
Definition 13 A tree is a poset
such that the
-predecessors of any element of the tree are well-ordered by

To any tree we can associate a rank function as usual,
For each the set of
with
is called the
-th level of the tree. The first
such that the
-th level of
is empty is called the height of
We are primarily interested in
-trees, i.e., trees of height
Definition 14 A branch through a tree
is a maximal linearly ordered subset of

Lemma 15 (König) Let
be an
-tree such that all its levels are finite (we say that
is infinite and finite branching). Then there is an infinite branch through

Proof: Define a branch by induction, so each
is in the
-th level of
and
is infinite.
Given define a tree
as follows: The nodes of the tree are the elements of
We define
by induction; in what follows,
refers always to the ordering of
rather than the usual
relation among integers. Denote by
the
-th level of
We define
by inductively defining the levels
Let
; the potential successors of
are the elements of
Given
and
let
be the set of potential successors of
Divide
into the
sets
for The immediate successors of
(all of which belong to
) are the least elements of these
sets (there may be less than
many of them, if one of the
is empty). The potential successors of
are the elements of
if any. This completes the construction of the tree. Notice that if
is infinite, at least one of the
is infinite as well. It follows that the tree
is an
-tree and that all its levels are finite; in fact,
for each
By König’s lemma, there is an infinite branch through
By construction, this branch is end-homogeneous, i.e., it has the property that for any
and any (larger) numbers
If this value is say that
is an
-node. Now apply the case
of the theorem: For some
the set
of
-nodes
is infinite, and we have ensured it is homogeneous for
This completes the proof of Ramsey’s theorem for
Assume Ramsey’s theorem for and let
By a further trivial induction, we may also assume that
We define an
-tree
all of whose levels are finite, and explain how to extract from any branch through
an infinite homogeneous set for
The first levels of
are simply given by
To choose the successors of
divide
into two classes,
and
and define as the set of least elements of each class (so
has size at most 2; it may be a singleton if one of the
is empty). Say
Then the elements of
are to be chosen among the remaining elements of
(if any).
Suppose we have already defined that
and that we have selected a subset
of
of potential successors of
Let
so
Define an equivalence relation on
by
The immediate successors of are the least elements of the
-equivalence classes, and the successors of any such element are to be chosen among the remaining elements of its class.
It follows that each node has finitely many immediate successors (since for each the equivalence relation
on
admits only finitely many classes). If
is infinite, at least one of the
-classes is infinite as well, and it follows that
is an
-tree. By König’s lemma, it has an infinite branch
Again,
is end-homogeneous: By construction,
has the property that given any
is constant for all
Say that is of type
if this value is 0 and of type
otherwise. This gives a coloring
By induction, there is an infinite
-homogeneous set
But then
is also
-homogeneous, and we are done.
2.4. Compactness
As it is well-known, an easy compactness argument shows that Ramsey’s theorem implies Theorem 4. The disadvantage of using compactness is that no discernible finite bounds seem to follow from such an argument:
Proof: We want to show that for all natural numbers there is an
such that
Suppose otherwise and fix counterexamples
so for all
there is a function
that does not admit homogeneous sets of size
Given two counterexamples
say that
iff
i.e., there must be integers
such that
and
This gives a tree structure to the set of all such functions. Notice that this tree is infinite, since there is a counterexample with domain for all
it is also finite branching, since there are only finitely many counterexamples with domain
for any given
because, in fact, there are only finitely many functions
By König’s lemma there is a branch through this tree. The functions along this branch cohere, and we can then define a function by taking their union. But, by construction,
does not admit a homogeneous set of size
which of course contradicts Ramsey’s theorem that claims that there must in fact be an infinite homogeneous set.
This is a typical example of a compactness argument, called this way because it can be recast as a corollary of the compactness of the Tychonoff product of certain finite (discrete) sets
It is also a consequence of the compactness of first-order logic. There is in fact a very general compactness result that applies even in situations where no tree argument as above is available.
Theorem 16 (Rado’s selection principle) Let
be a finite nonempty set for all
and let
For
set
and let
be given. Then there exists
such that for all
there is
such that
and
Proof: For let
and
We need to show that
This is an immediate consequence of Tychonoff’s theorem: Note that each is a closed subset of the Tychonoff product
of the discrete sets
because each
is finite, being a subset of the finite set
and we can write
as a finite union of closed sets. Let
We claim that has the finite intersection property. If this is the case, it follows from the compactness of
that
and we are done.
To prove the claim, let and let
for
be finite subsets of
Then
is finite, and
has an extension
By definition,
for all so
for all
and we are done.
Actually, we can quickly provide a self-contained proof of the remainder of the argument: Since has the finite intersection property, it can be extended to an ultrafilter
over
For
and
let
so for any fixed
This is a finite union, so it follows that for each
there is some
such that
Let
be the function
Then
as required: Let
Then
since is finite, all the
are in
and
In particular, this intersection is nonempty, and we can fix one of its elements, say
Then
and
Hence,
and we are done.
One can also prove Rado’s selection principle as a consequence of the compactness of first order logic; for example, it is easy to give a proof using the ultrapower construction as in the proof of 2 implies 6 of Theorem 8 in lecture II.11.
Theorem 4 is an easy consequence of Theorem 16: Given we want to show that for some
we have
Assume otherwise. It follows that for each finite
there is some function
without a homogeneous set of size
Let
and for each
let
For each
finite let
be
as above. For an arbitrary
pick some
finite such that
and let
be
Rado’s selection principle now gives us an
-coloring of
without homogeneous sets of size
as any such set would be contained in some
finite, such that
and we have a contradiction.
Another well-known consequence of Rado’s principle is the de Bruijn- theorem on the chromatic number of infinite graphs:
Definition 17 If
is a graph,
the chromatic number of
is the smallest cardinal
such that there is a map
where
is the set of vertices of
such that whenever
then there is no edge in
between
and
Theorem 18 (de Bruijn-
) Let
be a graph. If
and every finite subgraph
of
has chromatic number at most

then the same holds of


Proof: This is also an easy consequence of Theorem 16. Now take to be the set of vertices of
and each
to be
and take
for
to be a coloring witnessing that the chromatic number of the subgraph of
spanned by
is at most
Unlike the finite version of Ramsey’s theorem, the de Bruijn- result is not a consequence of König’s lemma, since
may well be uncountable. It follows immediately from Theorem 18 and the well-known 4-color theorem that every planar graph is 4-colorable.
A well-known open problem in geometric graph theory, the Hadwiger-Nelson problem, asks for the minimum number of colors required to color the plane such that no two points at distance one from each other have the same color. Abusing notation a bit, let’s call this number It is known that
the drawing below (taken from the wikipedia entry on the problem) shows both a coloring of the plane with 7 colors witnessing
and a finite graph showing that
Whatever the true value of Theorem 18 shows that any lower bound can be verified by examining some finite configuration. A recent remark of Shelah and Soifer suggests that the value of
may depend on whether the axiom of choice is adopted or not; Falconer has shown, for example, that
if we require the monochromatic sets to be Lebesgue measurable. In particular, this must be the case in Solovay’s model, or under determinacy, even if every finite subset of the plane has chromatic number at most 4.
Truszczynski-Tuza and Rav, among others, have studied consequences of Rado’s principle in algebra and combinatorics.
2.5. Ultrafilters
There is yet another proof of Ramsey’s theorem that is worth discussing. It explains that infinite homogeneous sets can be found because one of the colors is “large” in a precise sense. For this, we need a construction closely related to the product of ultrafilters discussed in lecture II.11.
It is convenient to think of ultrafilters (over in this discussion, but the argument holds in general) as generalized quantifiers: Let
be an ultrafilter over
. Given a formula
we interpret
as saying that “almost all”
have property
Clearly, we have:
-
-
- Similarly with any of the standard binary connectives in place of
Definition 19 Given a nonprincipal ultrafilter
over
and
, define
as the set of all
such that
Note that since
is nonprincipal. It then follows that for any
iff
Similarly,
is closed under finite intersections and supersets, so it is an ultrafilter. It is nonprincipal, since
for any finite
from which one easily gets that any
is infinite.
We now fix a nonprincipal and use
to give a proof that
In fact, given
we will obtain an infinite homogeneous set
such that
is contained in a color in
Without loss, we may assume that
- Note that there is a color
More precisely,
for some
Given
let
We then have:
-
whenever
where “” means “
”
Let Then:
-
- If
then
Hence we can build an increasing sequence such that for all
and all
we have
But then, letting
we have that
and we are done.
(Notice the similarities between this and the tree argument.)
Bibliography
Here are some additional references (besides those mentioned at the beginning) consulted while preparing this note:
- Paul
, George Szekeres, A combinatorial problem in geometry, Compositio Math. 2, (1935), 463–470.
- András Hajnal, Infinite combinatorics, in Handbook of combinatorics, Vol. 2, Elsevier (1995), 2085–2116.
- Walter Morris, Valeriu Soltan, The
-Szekeres problem on points in convex position—a survey, Bull. Amer. Math. Soc. (N.S.), 37 (4), (2000), 437–458.
- Frank Ramsey, On a problem of formal logic, Proc. London Math. Soc., 30, (1930), 264–286.
- Miroslaw Truszczynski, Zsolt Tuza, Rado’s Selection Principle: applications to binary relations, graph and hypergraph colorings and partially ordered sets, Discrete Mathematics, 103, (1992), 301–312.
Typeset using LaTeX2WP. Here is a printable version of this post.
Thank you for this introduction to partition calculus!
[…] Last lecture we showed that for any Later, we will see that for any and any there is such that On the other hand (recall we are assuming choice), there are no nontrivial positive partition relations with infinite. […]
Typo: In the proof in section 2.5, instead of it must be
it must be 
Fixed.[…] (Compare with the discussion of canonical relations in of lecture III.1.) […]
[…] the end-homogeneous sets approach, as in the proof of Ramsey’s theorem in Subsection 2.3 of lecture III.1. One can thus show the following: Theorem 3 (-Rado) Let and Let and let be an infinite […]
[…] (Compare with the discussion of canonical relations in of lecture III.1.) […]