Let me begin with a couple of comments that may help clarify some of the results from last lecture.
First, I want to show a different proof of Lemma 21.2, that I think is cleaner than the argument I gave before. (The argument from last lecture, however, will be useful below, in the proof of Kunen’s theorem.)
Lemma 1 If  is measurable,
is measurable, 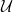 is a
is a  -complete nonprincipal ultrafilter over
-complete nonprincipal ultrafilter over  and
and  is the corresponding ultrapower embedding, then
is the corresponding ultrapower embedding, then 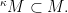
Proof: Recall that if 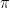 is Mostowski’s collapsing function and
is Mostowski’s collapsing function and ![{[\cdot]}](https://s0.wp.com/latex.php?latex=%7B%5B%5Ccdot%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) denotes classes in
denotes classes in  then
then ![{M=\{\pi([f]):f\in{}^\kappa V\}.}](https://s0.wp.com/latex.php?latex=%7BM%3D%5C%7B%5Cpi%28%5Bf%5D%29%3Af%5Cin%7B%7D%5E%5Ckappa+V%5C%7D.%7D&bg=ffffff&fg=000000&s=0&c=20201002) To ease notation, write
To ease notation, write  for
for ![{\pi([f]).}](https://s0.wp.com/latex.php?latex=%7B%5Cpi%28%5Bf%5D%29.%7D&bg=ffffff&fg=000000&s=0&c=20201002)
Let 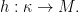 Pick
Pick  such that for all
such that for all 
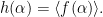
Lemma 2 With notation as above, 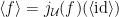 for any
for any 
Proof: For a set  let
let 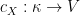 denote the function constantly equal to
denote the function constantly equal to  Since
Since 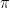 is an isomorphism,
is an isomorphism, 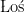 ‘s lemma gives us that the required equality holds iff
‘s lemma gives us that the required equality holds iff
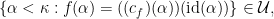
but this last set is just 

From the nice representation just showed, we conclude that 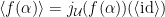 for all
for all  But for any such
But for any such 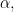
 because
because  by Lemma 21 from last lecture. Hence,
by Lemma 21 from last lecture. Hence, 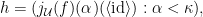 which is obviously in
which is obviously in 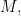 being definable from
being definable from 
 and
and 

The following was shown in the proof of Lemma 20, but it deserves to be isolated.
Lemma 3 If 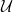 is a normal nonprincipal
is a normal nonprincipal  -complete ultrafilter over the measurable cardinal
-complete ultrafilter over the measurable cardinal  then
then  i.e., we get back
i.e., we get back 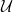 when we compute the normal measure derived from the embedding induced by
when we compute the normal measure derived from the embedding induced by 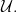

Finally, the construction in Lemma 10 and preceeding remarks is a particular case of a much more general result.
Definition 4 Given  and an ultrafilter
and an ultrafilter  over
over 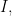 the projection
the projection 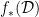 of
of  over
over 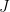 is the set of
is the set of  such that
such that 
Clearly, 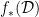 is an ultrafilter over
is an ultrafilter over 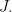
Notice that if 
 is a partition of
is a partition of 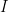 into sets not in
into sets not in  and
and  is given by
is given by  the unique
the unique 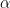 such that
such that  then
then 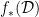 is a
is a  -complete nonprincipal ultrafilter over
-complete nonprincipal ultrafilter over  (Of course,
(Of course,  is possible.)
is possible.)
For a different example, let 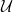 be a
be a  -complete nonprincipal ultrafilter over the measurable cardinal
-complete nonprincipal ultrafilter over the measurable cardinal  and let
and let  represent the identity in the ultrapower by
represent the identity in the ultrapower by 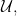
 Then
Then  is the normal ultrafilter over
is the normal ultrafilter over  derived from the embedding induced by
derived from the embedding induced by 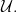
Definition 5 Given ultrafilters 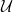 and
and  (not necessarily over the same set), say that
(not necessarily over the same set), say that 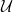 is Rudin-Keisler below
is Rudin-Keisler below 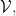 in symbols,
in symbols,  iff there are sets
iff there are sets 
 and a function
and a function 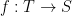 such that
such that 
Theorem 6 Let 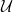 be an ultrafilter over a set
be an ultrafilter over a set  and
and  an ultrafilter over a set
an ultrafilter over a set  Suppose that
Suppose that  Then there is an elementary embedding
Then there is an elementary embedding 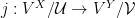 such that
such that 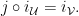
Proof: Fix  and
and  for which there is a map
for which there is a map 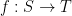 such that
such that  Clearly,
Clearly, 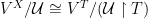 as witnessed by the map
as witnessed by the map ![{[f]_{\mathcal U}\mapsto[f\upharpoonright T]_{{\mathcal U}\upharpoonright T},}](https://s0.wp.com/latex.php?latex=%7B%5Bf%5D_%7B%5Cmathcal+U%7D%5Cmapsto%5Bf%5Cupharpoonright+T%5D_%7B%7B%5Cmathcal+U%7D%5Cupharpoonright+T%7D%2C%7D&bg=ffffff&fg=000000&s=0&c=20201002) and similarly
and similarly  so it suffices to assume that
so it suffices to assume that  and
and 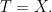
Given  let
let 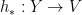 be given by
be given by  Then
Then ![{j([h]_{\mathcal U})=[h_*]_{\mathcal V}}](https://s0.wp.com/latex.php?latex=%7Bj%28%5Bh%5D_%7B%5Cmathcal+U%7D%29%3D%5Bh_%2A%5D_%7B%5Cmathcal+V%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) is well-defined, elementary, and
is well-defined, elementary, and 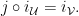
In effect,  iff
iff 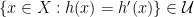 iff
iff  iff
iff  where the second equivalence holds by assumption, and it follows that
where the second equivalence holds by assumption, and it follows that  is well-defined.
is well-defined.
If  denotes the function with domain
denotes the function with domain  and constantly equal to
and constantly equal to  then for any
then for any 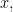
![{j\circ i_{\mathcal U}(x)=j([c^X_x]_{\mathcal U})=[(c^X_x)_*]_{\mathcal V}=[c^Y_x]_{\mathcal V}=i_{\mathcal V}(x)}](https://s0.wp.com/latex.php?latex=%7Bj%5Ccirc+i_%7B%5Cmathcal+U%7D%28x%29%3Dj%28%5Bc%5EX_x%5D_%7B%5Cmathcal+U%7D%29%3D%5B%28c%5EX_x%29_%2A%5D_%7B%5Cmathcal+V%7D%3D%5Bc%5EY_x%5D_%7B%5Cmathcal+V%7D%3Di_%7B%5Cmathcal+V%7D%28x%29%7D&bg=ffffff&fg=000000&s=0&c=20201002) since
since 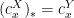 by definition of the map
by definition of the map  This shows that
This shows that 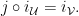
Elementarity is a straightforward modification of the proof of Lemma 10 from last lecture. 
One can show that Theorem 6 “very nearly” characterizes the Rudin-Keisler ordering, see for example Proposition 0.3.2 in Jussi Ketonen, Strong compactness and other cardinal sins, Annals of Mathematical Logic 5 (1972), 47–76.
Read the rest of this entry »
is consistent with the other axioms of set theory. Gödel’s argument goes well beyond this result; his identification of the class
of constructible sets eventually led to the development of inner model theory, one of the main areas of active research within set theory nowadays.
is defined as
for
limit, and
where



 Posted by andrescaicedo
Posted by andrescaicedo