580 -Partition calculus (4)

April 9, 2009

 

1. Colorings of pairs. I

 

There are several possible ways in which one can try to generalize Ramsey’s theorem to larger cardinalities. We will discuss some of these generalizations in upcoming lectures. For now, let’s highlight some obstacles.

Theorem 1 ({\mbox{Erd\H os}}-Kakutani) {\omega_1\not\rightarrow(3)^2_\omega.} In fact, {2^\kappa\not\rightarrow(3)^2_\kappa.}

 

Proof: Let {S={}^\kappa\{0,1\}.} Let {F:[S]^2\rightarrow\kappa} be given by

\displaystyle F(\{f,g\})=\mbox{least }\alpha<\kappa\mbox{ such that }f(\alpha)\ne g(\alpha).

Then, if {f,g,h} are distinct, it is impossible that {F(\{f,g\})=F(\{f,h\})=F(\{g,h\}).} \Box

Theorem 2 (Sierpi\’nski) {\omega_1\not\rightarrow(\omega_1)^2.} In fact, {2^\kappa\not\rightarrow(\kappa^+)^2.}

 

Proof: With {S} as above, let {F:[S]^2\rightarrow2} be given as follows: Let {<} be a well-order of {S} in order type {2^\kappa.} Let {<_{lex}} be the lexicographic ordering on {S.} Set

\displaystyle F(\{f,g\})=1\mbox{ iff }<_{lex}\mbox{ and }<\mbox{ coincide on }\{f,g\}.

Lemma 3 There is no {<_{lex}}-increasing or decreasing {\kappa^+}-sequence of elements of {S.}

 

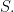
Proof: Let {W=\{f_\alpha\colon\alpha<\kappa^+\}} be a counterexample. Let {\gamma\le\kappa} be least such that {\{f_\alpha\upharpoonright\gamma\colon\alpha<\kappa^+\}} has size {\kappa^+,} and let {Z\in[W]^{\kappa^+}} be such that if {f,g\in Z} then {f\upharpoonright\gamma\ne g\upharpoonright\gamma.} To simplify notation, we will identify {Z} and {W.} For {\alpha<\kappa^+} let {\xi_\alpha<\gamma} be such that {f_\alpha\upharpoonright\xi_\alpha=f_{\alpha+1} \upharpoonright\xi_\alpha} but {f_\alpha(\xi_\alpha)=1-f_{\alpha+1}(\xi_\alpha).} By regularity of {\kappa^+,} there is {\xi<\gamma} such that {\xi=\xi_\alpha} for {\kappa^+} many {\alpha.}

But if {\xi=\xi_\alpha=\xi_\beta} and {f_\alpha\upharpoonright\xi=f_\beta\upharpoonright\xi,} then {f_\beta<_{lex} f_{\alpha+1}} iff {f_\alpha<_{lex} f_{\beta+1},} so {f_\alpha=f_\beta.} It follows that {\{f_\alpha\upharpoonright\xi\colon\alpha<\kappa^+\}} has size {\kappa^+,} contradicting the minimality of {\gamma.} \Box

The lemma implies the result: If {H\subseteq S} has size {\kappa^+} and is {F}-homogeneous, then {H} contradicts Lemma 3. \Box

Now I want to present some significant strengthenings of the results above. The results from last lecture exploit the fact that a great deal of coding can be carried out with infinitely many coordinates. Perhaps surprisingly, strong anti-Ramsey results are possible, even if we restrict ourselves to colorings of pairs.

Read the rest of this entry »

3 Comments | 580: Topics in set theory | Tagged: , , , , , , , , , , , , | Permalink
Posted by andrescaicedo

580 -Cardinal arithmetic (5)

February 13, 2009

At the end of last lecture we defined club sets and showed that the diagonal intersection of club subsets of a regular cardinal is club.

Definition 10. Let \alpha be a limit ordinal of uncountable cofinality. The set S\subseteq\alpha is stationary in \alpha iff S\cap C\ne\emptyset for all club sets C\subseteq\alpha. 

For example, let \lambda be a regular cardinal strictly smaller than {\rm cf}(\alpha). Then S^\alpha_\lambda:=\{\beta<\alpha : {\rm cf}(\beta)=\lambda\} is a stationary set, since it contains the \lambda-th member of the increasing enumeration of any club in \alpha. This shows that whenever {\rm cf}(\alpha)>\omega_1, there are disjoint stationary subsets of \alpha. Below, we show a stronger result. The notion of stationarity is central to most of set theoretic combinatorics. 

Fact 11. Let S be stationary in \alpha.

  1. S is unbounded in \alpha.
  2. Let C be club in \alpha. Then S\cap C is stationary. 

Proof. 1. S must meet \kappa\setminus\alpha for all \alpha and is therefore unbounded.

2. Given any club sets C and D, (S\cap C)\cap D=S\cap(C\cap D)\ne\emptyset, and it follows that S\cap C is stationary. {\sf QED}

Read the rest of this entry »

6 Comments | 580: Topics in set theory | Tagged: , , , , , , | Permalink
Posted by andrescaicedo