This continues the previous post on Friedman’s theorem.
I want to give a brief idea of the size of Friedman’s 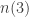 , as defined on homework 2. The reference for what follows is
, as defined on homework 2. The reference for what follows is
- Harvey Friedman, Long finite sequences, J. Combin. Theory Ser. A, 95 (1) (2001), 102–144.
Recall that 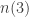 is the largest possible size
is the largest possible size  of a sequence
of a sequence  with property
with property  , all of whose terms are 1, 2, or 3. Here, to have property
, all of whose terms are 1, 2, or 3. Here, to have property  means that if
means that if 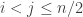 , then the sequence
, then the sequence  is not a subsequence of the sequence
is not a subsequence of the sequence 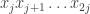 .
.
In lecture we gave an example of such a sequence, of length 216, namely
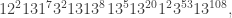
where we use exponential notation to indicate the number of times a symbol appears consecutively, so the sequence begins
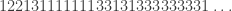
Actually, 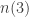 is much larger than 216. We know it is finite but, as Friedman mentions in his paper, it is an incomprehensibly large number. To explain this, we should mention the Ackermann hierarchy of functions. These are functions
is much larger than 216. We know it is finite but, as Friedman mentions in his paper, it is an incomprehensibly large number. To explain this, we should mention the Ackermann hierarchy of functions. These are functions  , with each
, with each  a strictly increasing function.
a strictly increasing function.
Define  . Also, set
. Also, set
 ,
,
where there are  occurrences of
occurrences of 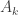 .
.
This is perhaps best understood by computing a few examples. We have  ,
, 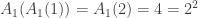 ,
,  and, by an easy induction,
and, by an easy induction,  .
.
Now,  ,
,  ,
, 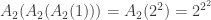 and, in general,
and, in general,  is an exponential tower of 2s of height
is an exponential tower of 2s of height  .
.
The descriptions become more complicated now. For example,  is an exponential tower of 2s, but its height is itself an exponential tower of 2s (of height
is an exponential tower of 2s, but its height is itself an exponential tower of 2s (of height  ). For example,
). For example,
 ,
,
where the tower has height 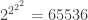 .
.
Let me now quote from Friedman’s paper:
I submit that  is a ridiculously large number, but it is not an incomprehensibly large number. One can imagine a tower of 2’s of a large height, where that height is 65,536, and 65,536 is not ridiculously large.
is a ridiculously large number, but it is not an incomprehensibly large number. One can imagine a tower of 2’s of a large height, where that height is 65,536, and 65,536 is not ridiculously large.
However, if we go much further, then a profound level of incomprehensibility emerges. The definitions are not incomprehensible, but the largeness is incomprehensible. These higher levels of largeness blur, where one is unable to sense one level of largeness from another.
For instance,  is an exponential tower of 2’s of height
is an exponential tower of 2’s of height  .
.
It seems safe to assert that, say,  is incomprehensibly large. We propose this number as a sort of benchmark. In Section 4 we prove that
is incomprehensibly large. We propose this number as a sort of benchmark. In Section 4 we prove that  , which is considerably larger.
, which is considerably larger.
Friedman actually goes much further than this. Using computer data provided by Randall Dougherty, Friedman proves in the last section of the paper that
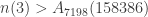 .
.
For all I know, this could still be very far from the actual value of 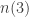 . And I do not know a reasonable description of an upper bound.
. And I do not know a reasonable description of an upper bound.
In technical terms, Friedman proves that the function 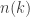 is not primitive recursive, and actually grows much faster than the usual examples of recursive functions that are not primitive recursive. He also describes a function
is not primitive recursive, and actually grows much faster than the usual examples of recursive functions that are not primitive recursive. He also describes a function  (a member of the so-called Hardy hierarchy) that grows faster than
(a member of the so-called Hardy hierarchy) that grows faster than 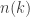 . This means that
. This means that 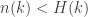 for all sufficiently large
for all sufficiently large  , but the argument does not give a specific bound when
, but the argument does not give a specific bound when 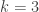 .
.
43.614000
-116.202000
, the symmetric and alternating groups in
letters.
.
, the group of all invertible
matrices with real entries, or
, the group of all
matrices with real entries and determinant 1.



 Posted by andrescaicedo
Posted by andrescaicedo 